Guía n° 5 de ejercicios de funciones Integrales
Resolver los siguientes ejercicios
Fórmulas aplicables:
Si:
| w(x) = ∫ | y2(x) | f(x, y)·dy |
| y1(x) |
Entonces:
| d dx | = ∫ | y2(x) | f(x, y)·dy = ∫ | y2(x) | fx(x, y)·dy - f(x, y1(x))· | dy1 dx | + f(x, y2(x))· | dy2 dx |
| y1(x) | y1(x) |
Calcular, con la regla de la cadena, las derivadas parciales primeras de las siguientes funciones:
Problema n° 11
| f(x, y) = ∫ | π | yx + 3·cos t²·dt |
| sen x |
Problema n° 12
| f(x, y) = ∫ | cos x | arcsen (x·y·t)·dt |
| sen x |
Problema n° 13
| f(x, y) = ∫ | x | arctg (y + 2·t)·dt |
| cos y |
Problema n° 14
| f(x, y) = ∫ | y·sen² x | ex² 1 + t² | ·dt |
| x·cos² y |
Problema n° 15
| f(x, y) = ∫ | ey | (x² + t³·log y)·dt |
| x² + y² |
Problema n° 16
| f(x, y) = ∫ | ex·y | x·y·z·dz |
| x² + y² |
Problema n° 17
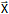| f(x, y) = ∫ | √x | cos(y²·z²)·dz |
| 1 |
Problema n° 18
| f(x, y) = ∫ | e | yx·log² z·dz |
| x² - 1 |
Problema n° 19
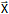| f(x, y) = ∫ | ∛x | sen (x4·y·z²)·dz |
| x·y |
Problema n° 20
| f(x, y) = ∫ | arcsen x | e-y·z²·dz |
| e |
Autor: Ricardo Santiago Netto (Administrador de Fisicanet)
San Martín. Buenos Aires. Argentina.
Ver condiciones para uso de los contenidos de fisicanet.com.ar
• Fuente:
Ejercicios extraídos del libro "Lecciones de AnáLisis II" del Dr. Alfredo F. Novelli para Análisis Matemático II de UNLu.