• • Página de inicio
• › Análisis Matemático
• › Integrales
• › Trabajo práctico TP04
• › Ejercicio n° 5

Ejemplo, cómo calcular la integral sobre una curva.

Problema n° 5 de integrales

Enunciado del ejercicio n° 5

Calcular la posición del baricentro de un alambre semicircular homogéneo de radio R.

La posición del baricentro será:

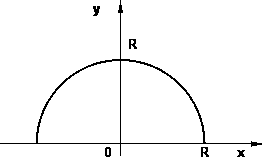
Gráfico del dominio para el cálculo de baricentro

Según el enunciado se trata de una semicircunferencia que ubicamos por comodidad con su centro en el origen de coordenadas, de modo que una de las coordenadas del baricentro se encontrará sobre uno de los ejes por simetría del dominio y antisimetría de la integranda.

Parametrizando:

C(t) = (R·cos t, R·sen t) ⇒ 0 ≤ t ≤ π

Así X_G = 0

Luego:

Y_G = l/longitud

Calculando las partes:

C'(t) = (-R·sen t, R·cos t)

||C'(t)|| = √(-R·sen t)² + (R·cos t)²

||C'(t)|| = √R²·sen² t + R²·cos² t

||C'(t)|| = √R²·(sen² t + cos² t)

||C'(t)|| = √R²

||C'(t)|| = R

f(X) = y ⇒ f(C(t)) = R·sen t

I = ∫_C y·ds

I = R²·[-cos π - (-cos 0)]

I = R²·[-(-1) - (-1)]

I = R²·(1 +1)

I = 2·R²

Longitud = ∫_C ds

Longitud = R·π

Y_G = 2·R²/R·π = 2·R/π

El baricentro es:

G = (0, 2·R/π)

• ‹ Anterior
• |
• Regresar a la guía TP04
• |
• Siguiente ›

Ver condiciones para uso de los contenidos de fisicanet.com.ar

• 🔍
• ✉ f t