Problema nº 5 de operaciones con números reales, suma, resta, potenciación y radicación - TP10
Resolver los siguientes ejercicios
Problema nº 5
Calcular:
a)
8⅓ = (2³)⅓ =
Potencia de potencia los exponentes se multiplican:
= 23·⅓ = 2¹
8⅓ = 2
b)
81⁻0,25 =
Expresamos el exponente como número fraccionario:
= 81⁻25/100 =
Expresamos la base como potencia y simplificamos el exponente:
= (3⁴)⁻¼ =
Potencia de potencia los exponentes se multiplican:
= 34·(-1/4) = 3⁻¹
| 81⁻0,25 = | 1 |
| 3 |
c)
1250,33... =
Expresamos el exponente como número fraccionario:
= 125⅓ =
Expresamos la base como potencia:
= (5³)⅓ =
Potencia de potencia los exponentes se multiplican:
= 53·⅓ = 5¹
1250,33... = 5
d)
5·5⅓÷5⅙ =
Las bases son iguales, los exponentes se suman:
| 1 + | 1 | - | 1 | = | 6 + 2 - 1 | = | 7 |
| 3 | 6 | 6 | 6 |
= 57/6 = ⁶√5⁷ = ⁶√5·5⁶
Extraemos de la raíz 5⁶:
= 5·⁶√5
5·5⅓÷5⅙ = 5·⁶√5
e)
| π½ + π⁻½ | = |
| π½ - π⁻½ |
Multiplicamos y dividimos por "π½ + π⁻½":
| = | π½ + π⁻½ | · | π½ + π⁻½ | = |
| π½ - π⁻½ | π½ + π⁻½ |
En el denominador tenemos una diferencia de cuadrados de igual base:
| = | (π½ + π⁻½)² | = |
| (π½)² - (π⁻½)² |
En el numerador desarrollamos el binomio al cuadrado, donde corresponda aplicamos potencia de potencia:
| = | (π½)² + 2·π½·π⁻½ + (π⁻½)² | = |
| π2·½ - π2·(-½) |
Donde las bases sean iguales los exponentes se suman:
| = | π2·½ + 2·π½ + (-½) + π2·(-½) | = |
| π¹ - π⁻¹ |
| = | π¹ + 2·π½ - ½ + π⁻¹ | = |
| π - π⁻¹ |
| = | π + 2·π⁰ + π⁻¹ | = | π + 2·1 + π⁻¹ | = |
| π - π⁻¹ | π - π⁻¹ |
Invertimos las potencias con exponente negativo:
| = | π + 2 + | 1 | = |
| π | |||
| π - | 1 | ||
| π |
Sumamos las fracciones en el numerador y en el denominador:
| = | π·π + 2·π + 1 | = |
| π | ||
| π·π - 1 | ||
| π |
Simplificamos:
| = | π² + 2·π + 1 | = |
| π | ||
| π² - 1 | ||
| π |
| = | π² + 2·π + 1 | = |
| π² - 1 |
En el numerador hay un trinomio cuadrado perfecto y en el denominador hay una diferencia de cuadrados de igual base, factorizamos:
| = | (π + 1)² | = |
| (π - 1)·(π + 1) |
Simplificamos:
| = | (π + 1)2 | = | π + 1 |
| (π - 1)·(π + 1) | π - 1 |
| π½ + π⁻½ | = | π + 1 |
| π½ - π⁻½ | π - 1 |
f)
√½·a³·5·∛2⁴·a⁻¹ =
Expresamos las raíces como potencias:
= (½·a³)½·5·(2⁴·a⁻¹)⅓ =
Aplicamos distributiva a los exponentes principales:
= ½½·(a³)½·5·(2⁴)⅓·(a⁻¹)⅓ =
Efectuamos potencia de potencia:
= ½½·a3·½·5·24·⅓·a(-1)·⅓ = 2⁻½·a3/2·5·24/3·a⁻⅓ =
Donde las bases son iguales sumamos los exponentes:
= 2⁻1/2 + 4/3·a3/2 - ⅓·5 =
Para la potencia de base "2":
| - | 1 | + | 4 | = | -3 + 8 | = | 5 |
| 2 | 3 | 6 | 6 |
Para la potencia de base "a":
| 3 | - | 1 | = | 9 - 2 | = | 7 |
| 2 | 3 | 6 | 6 |
Queda:
= 2⅚·a7/6·5 =
= 2⅚·a⅙·a6/6·5 =
= 2⅚·a⅙·a·5 =
Agrupamos:
= (2⁵·a)⅙·5 =
Expresamos las potencias como raíces:
= ⁶√2⁵·a·a·5
√½·a³·5·∛2⁴·a⁻¹ = ⁶√2⁵·a·a·5
g)
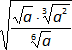 =
=
Expresamos las raíces como potencias:
= 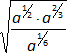 =
=
Las bases son iguales, los exponentes se suman:
| 1 | + | 2 | - | 1 | = | 3 + 4 - 1 | = | 6 | = 1 |
| 2 | 3 | 6 | 6 | 6 |
= √a¹
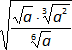 = √a
= √a
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP10
- | Siguiente ›
Ejemplo de suma, resta, potenciación y radicación con números reales