Problema nº 4 de operaciones con números reales, racionalización de denominadores - TP10
Resolver los siguientes ejercicios
Problema nº 4
Racionalizar los denominadores de las siguientes fracciones:
a)
Multiplicamos y dividimos por "√5":
b)
Multiplicamos y dividimos por "√3 + √2", aplicando diferencia de cuadrados:
| = | 1 | · | √3 + √2 | = |
| √3 - √2 | √3 + √2 |
| = | √3 + √2 | = |
| (√3 - √2)·(√3 + √2) |
c)
Multiplicamos y dividimos por "√√2 - 1":
| = | √√2 + 1 | · | √√2 - 1 | = |
| √√2 - 1 | √√2 - 1 |
| = | (√√2 + 1)·(√√2 - 1) | = |
| (√√2 - 1)·(√√2 - 1) |
| = | √(√2 + 1)·(√2 - 1) | = |
| (√√2 - 1)² |
Multiplicamos y dividimos por "√2 + 1":
| = | (√3)·(√2 + 1) | = |
| (√2 - 1)·(√2 + 1) |
d)
Multiplicamos y dividimos agrupando los términos del denominador de forma conveniente para eliminar una raíz "(√3) + (√2 - 1)":
| = | √3 | · | √3 + (√2 - 1) | = |
| √3 - √2 - 1 | √3 + (√2 - 1) |
| = | √3·(√3 + √2 - 1) | = |
| [√3 - (√2 - 1)]·[√3 + (√2 - 1)] |
| = | √3·√3 + √3·√2 - √3 | = |
| (√3)² - (√2 - 1)² |
| = | (√3)² + √3·√2 - √3 | = |
| 3 - [(√2)² - 2·√2·1 + 1²] |
| = | 3 + √3·√2 - √3 | = |
| 3 - (2 - 2·√2 + 1) |
| = | 3 + √3·√2 - √3 | = |
| 3 - 2 + 2·√2 - 1 |
Multiplicamos y dividimos por "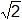 ":
":
| = | 3 + √3·√2 - √3 | · | √2 | = |
| 2·√2 | √2 |
| = | (3 + √3·√2 - √3)·√2 | = |
| 2·√2·√2 |
| = | 3·√2 + √3·√2·√2 - √3·√2 | = |
| 2·(√2)² |
| = | 3·√2 + √3·(√2)² - √3·2 | = |
| 2·2 |
| √3 | = | 3·√2 + 2·√3 - √6 |
| √3 - √2 - 1 | 4 |
e)
Multiplicamos y dividimos por "⁹√2⁴":
| = | 2·⁹√2⁴ | = | 2·⁹√2⁴ | = | 2·⁹√2⁴ |
| ⁹√2⁵·2⁴ | ⁹√2⁹ | 2 |
f)
Para poder racionalizar un denominador la condición básica es el radicando sea una potencia donde el exponente sea igual al índice de la raíz. De tal forma que la raíz expresada como potencia logre un exponente igual a 1.
Expresamos la raíz como potencia:
Entonces p/n = 1 con la condición dada de n > p, la forma más simple de lograrlo es con el opuesto multiplicativo:
Por lo tanto, multiplicamos y dividimos por "ᵖ√aⁿ":
Resolvió: Ricardo Santiago Netto. Argentina
Ejemplo de operaciones de racionalización de denominadores
![]() ":
":