Guía nº 14-c de ejercicios de operaciones con números reales
División de radicales
a)
Para dividir radicales del mismo índice; se dividen previamente los signos, luego los coeficientes entre sí y finalmente bajo un mismo radical común se dividen las cantidades sub-radicales entre sí. A continuación se efectúa las operaciones indicadas dentro del radical y se extraen los factores posibles fuera del radical si los hubiera.
Ejercicio de aplicación:
Dividir los siguientes radicales indicados:
1) 4·√6÷2·√3 =
2) 2·√50÷6·√24 =
3) 20·√2÷2·√4 =
4) 12·√3÷4·√3 =
5) √18÷√25 =
6) 7·√13÷28·√26 =
7) -9·√8÷√2 =
8) -2·√50÷(-√5) =
9) ∛88÷∛11 =
10) ∛5÷∛3 =
11) 2·√3·a÷10·√a =
12) √75·x²·y³÷5·√3·x·y =
13) 4·x·√a³·x²÷√a²·x³ =
14) ½·√3·x·y÷¿·√x =
15) ⅗·a·b·√12·x⁻⁴·y³·z÷(-√6·x²·y⁵) =
16) 3·∛16·a⁵÷4·∛2·a² =
17) 2·∛81·x²÷3·∛3·x² =
18) (-2·∛5·x¹¹·y¹⁰·z⁵)÷(-¼·∛0,1·x⁻⁴·y³·z⁷) =
19) ⅔·a·∛x²÷(a/3·x²)·∛x³ =
20) (-½·∜x³)÷∜16·x⁻⁵ =
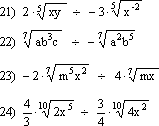
b)
Para dividir radicales de distinto índice; primeramente se reducen los radicales al mínimo común índice y luego se dividen como si fueran radicales del mismo índice.
Ejercicio de aplicación:
Dividir los siguientes radicales indicados:
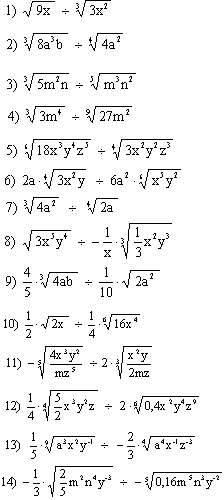
Racionalización
Es una operación que tiene por objeto cancelar siempre el radical del denominador.
1er Caso: cuando el radical del denominador es de 2do grado, es decir posee como radical una raíz cuadrada.
Ejemplos:
| I) | 3 | = | 3 | · | √6 | = | 3·√6 | = | 3·√6 | = | √6 |
| √6 | √6 | √6 | (√6)² | 6 | 2 |
| II) | y | = | y | · | √2 | = | y·√2 | = | y·√2 |
| √2 | √2 | √2 | (√2)² | 2 |
| III) | n | = | n | · | √a | = | n·√a | = | n·√a |
| √a | √a | √a | (√a)² | a |
| IV) | x | = | x | · | √x | = | x·√x | = | x·√x | = | √x |
| 4·√x | 4·√x | √x | 4·(√x)² | 4·x | x |
Observación: Para racionalizar el denominador de una fracción bastará multiplicar la fracción por el factor racionalizante del denominador, en éste caso por sí mismo.
2do Caso: cuando el radical del denominador es mayor al de 2do grado, es decir radicales de 3er,4to, 5to y más grado.
Ejemplos:
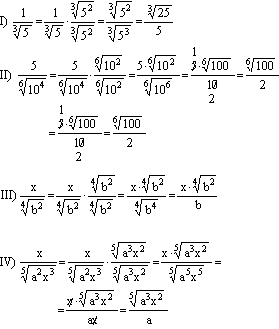
Observación: Para racionalizar el denominador de una fracción bastará multiplicar la fracción por el radical del mismo índice con la misma cantidad sub-radical pero el exponente de la cantidad sub-radical debe expresar la diferencia que existe entre el índice del radical y el exponente de la cantidad sub-radical.
3er Caso: cuando el radical del denominador es un binomio.
Ejemplos:
| I) | √7 - √2 | = | (√7 - √2)·(√7 - √2) | = | 9 - 2·√14 |
| √7 + √2 | (√7 + √2)·(√7 - √2) | 5 |
| II) | 4 | = | 4·(3·√2 + √5) | = | 4·(3·√2 - √5) |
| 3·√2 - √5 | (3·√2 - √5)·(3·√2 + √5) | 13 |
| III) | a | = | a·(√m + √n) | = | a·(√m - √n) |
| √m + √n | (√m + √n)·(√m - √n) | m - n |
| IV) | 9·√x | = | 9·√x·(x + √x) | = | 9·x·√x + 9·x | = | 9·x·(√x + 1) | = | 9·(√x + 1) |
| x - √x | (x - √x)·(x + √x) | x² - x | x·(x - 1) | x - 1 |
Observación: Para racionalizar el denominador de una fracción bastará multiplicar la fracción por la conjugada del denominador.
Se llaman cantidades conjugadas a 2 binomios que tienen las mismas cantidades literales, los mismos coeficientes y los mismos exponentes, diferenciando solamente en el signo del 2do término del 2do binomio.
Autor: Hugo David Giménez Ayala. Paraguay.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).