Matrices y determinantes. Operaciones (segunda parte)
Cálculo del rango de una matriz
Consideremos la matriz A = (aij):
A =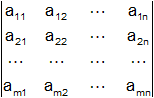 
1) El rango de la matriz A coincide con el de la matriz A' que se obtiene suprimiendo en la matriz A todas la líneas (filas o columnas) cuyas entradas estén sólo formadas por ceros, es decir, que sean nulas.
2) Consideremos la matriz:
A₁ = (a₁₁, a₁₂, …, a₁ₙ)
Y supongamos que a₁₁ ≠ 0, entonces:
Rango (A) ≥ rango (A₁) = 1
3) Añadimos filas de la matriz A a la matriz A₁ hasta encontrar una matriz que cumpla:
A₂ = 
, donde (1 < i ≤ n),:
Tal que posea un menor no nulo de la forma:
≠ 0
Por consiguiente,
rango (A) ≥ rango (A₂) = 2.
Si esto no hubiese sido posible, entonces:
rango (A) = 1.
Supongamos que rango (A) ≥ rango (A₂) y que i = 2 y j = 2.
4) Añadimos filas a la matriz A₂ hasta encontrar una matriz que cumpla:
A₃ =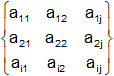 
De forma que posea un menor de orden tres de la forma:
≠ 0
Entonces:
rango (A) ≥ rango (A₂) = 3.
En caso de no haber sido posible encontrar dicho menor, entonces:
rango (A) = rango (A₂) = 2.
Suponiendo que rango (A) ≥ rango (A₃) y que i = 3 y j = 3, se procedería como en los casos anteriores, y así sucesivamente hasta agotar todas las filas de la matriz A.
Ejemplos:
a)
Sea la matriz A una matriz de orden tres. Hallar el rango (A).
A =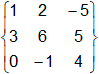 
Como A es una matriz cuadrada de orden tres, como máximo el rango (A) puede valer tres. Calcularemos primero el determinante o determinantes de las submatrices de orden dos de A. Así pues
= 6 - 6 = 0
Ya que el resultado es cero, probaremos con todas las submatrices de A hasta encontrar una cuyo determinante no sea cero. Si no encontramos ninguna, el rango (A) = 1.
= 2 - (-15) = 2 + 15 = 17 ≠ 0
Puesto que el resultado de calcular el determinante de esta submatriz de A no es nulo, podemos afirmar de momento que el rango (A) = 2.
Añadimos ahora una columna y una fila más para ver si el rango puede ser tres:
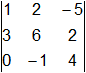= 24 + 0 + 15 - 0 - 24 + 2 = 17 ≠ 0
Dado que el determinante de A no es nulo y a su vez es de orden tres, el rango
(A) = 3.
No necesariamente para poder calcular el rango de una matriz, ésta tiene que ser cuadrada. Así, en el siguiente ejemplo:
b)
Calcular el rango de la matriz B de orden 3×4.
B =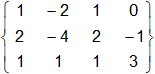 
= -4 + 4 = 0
= -1 + 0 = -1 ≠ 0
= -1 + 0 = -1 ≠ 0
Como hay una determinante de orden dos no nulo, el rango de la matriz B es mayor o igual que 2. Calculamos a continuación los determinantes de orden superior:
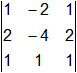= -4 - 4 + 2 + 4 + 4 - 2 = 0
Probamos con un segundo determinante de orden tres:
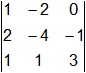= -12 + 2 + 0 + 0 + 12 + 1 = 3 ≠ 0
Así pues, como hay un determinante de orden tres que no es nulo, el rango (B) = 3. Un rango mayor que 3 no se puede hallar, ya que no se puede formar un determinante de orden 4. Recuérdese que para poder calcular el determinante de una matriz o de una submatriz, éstas tienen que ser cuadradas.
Autor: Jesús. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).