Matrices y determinantes. Operaciones (primera parte)
Adjunto de una matriz
Consideremos una matriz n-cuadrada A = (aₓ) sobre un cuerpo K. El adjunto de A, denotado por adj A, es la traspuesta de la matriz de cofactores de A:
adj A =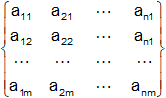 
Ejemplo:
Sea A =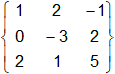 
Los cofactores de los nueve elementos de A son:
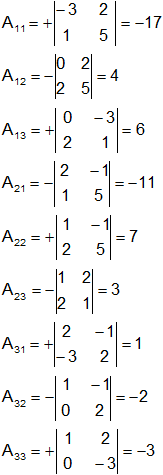
La traspuesta de la matriz de los cofactores anteriores proporciona el adjunto de A:
adj A =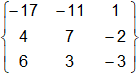 
Aplicación del adjunto para hallar la matriz inversa.
Para toda matriz cuadrada A, A·(adj A) = (adj A)·A = |A| I
De este modo, si |A| ≠ 0,
A⁻¹ = 1/|A| (Adjunta A)
Observemos que esta propiedad nos permite hallar por otro método la inversa de una matriz.
Ejemplo:
Consideremos la matriz
A =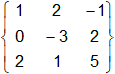
y
adj A =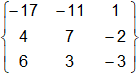
y el det A:
det (A) =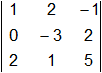 
= -15 + 8 + 0 - 6 - 0 - 2
det (A) = -15 ≠ 0
Así pues, aplicando la propiedad anterior:
A⁻¹ = 1/|A| (Adjunta A), obtenemos:
A⁻¹ = (-1/15)·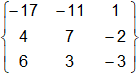
Ejemplo de cálculo de la matriz inversa
Ejemplo nº 1
Calcular, por la propiedad anterior, la inversa de las siguientes matrices:
a)
b)
A =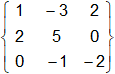 
a)
Primero hallaremos el determinante de la matriz A:
det A = 
= 0
Como el determinante es cero, no existe la inversa de la matriz A
det B = 
= 15 + 2 = 17
El siguiente paso es hallar el adjunto de la matriz B, así pues, los cofactores de los cuatro elementos de B son:
B₁₁ = 5
B₁₂ = -2
B₂₁ = 1
B₂₂ = 3
y el adjunto de B, denotado por adj B, será
adj B = 
Aplicando ahora la propiedad
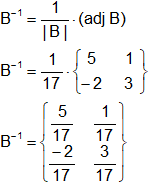
b)
Empezaremos por hallar el det A,
det A =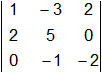 
= -10 - 4 - 12 = -26
Los cofactores de los nueve elementos de A son:
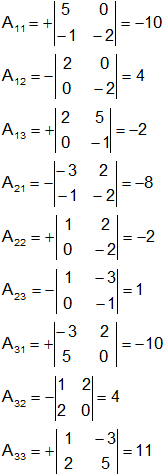
La traspuesta de la matriz de los cofactores anteriores proporciona el adjunto de A:
adj A =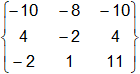 
Aplicando la propiedad de la matriz inversa obtenemos A⁻¹:
A⁻¹ = 1/|A| (Adjunta A)
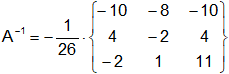
Simplificando:
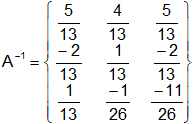
Autor: Jesús. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).