Ejemplo, cómo calcular los lados y los ángulos de triángulos mediante trigonometría

Problema n° 1 de trigonometría - TP06

Enunciado del ejercicio n° 1

Resolver el triángulo rectángulo de la figura, utilizando los datos que se indican en cada caso:

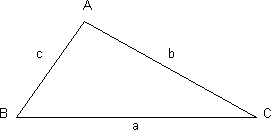
Desarrollo

Datos:

Fórmulas:

A + B + C = 180° (suma de los ángulos interiores de un triángulo)

sen θ = Cateto opuesto/Hipotenusa.

cos θ = Cateto adyacente/Hipotenusa.

tg θ = Cateto opuesto/Cateto adyacente

h² = a² + b² (Teorema de Pitágoras)

Solución

a)

Recordamos la tabla:

A + B + C = 180°

C = 180° - A - B

C = 180° - 90° - 35° 15'

C = 54° 45'

sen B = c/a

c = a·sen B

c = (120 m)·sen 35° 15'

c = (120 m)·0,5771

c = 69,25 m

cos B = b/a

b = a·cos B

b = (120 m)·cos 35° 15'

b = (120 m)·0,8166

b = 98,00 m

b)

A + B + C = 180°

B = 180° - A - C

B = 180° - 90° - 15° 18' 32"

B = 74° 41' 28"

sen C = b/a

b = a·sen C

b = (3.500 m)·sen 15° 18' 32"

b = (3.500 m)·0,2640

b = 924,08 m

cos C = c/a

c = a·cos C

c = (3.500 m)·cos 15° 18' 32"

c = (3.500 m)·0,9645

c = 3.375,81 m

c)

A + B + C = 180°

C = 180° - A - B

C = 180° - 90° - 72° 10'

C = 17° 50'

cos B = c/a

a = c/cos B

a = (130 m)/cos 72° 10'

a = (130 m)/0,3062

a = 424,49 m

tg B = b/c

b = c·tg B

b = (130 m)·tg 72° 10'

b = (130 m)·3,1084

b = 404,09 m

d)

A + B + C = 180°

C = 180° - A - B

C = 180° - 90° - 29° 12' 15"

C = 60° 47' 45"

sen B = b/a

a = b/sen B

a = (239 m)/sen 29° 12' 15"

a = (239 m)/0,4879

a = 489,83 m

tg B = b/c

c = b/tg B

c = (239 m)/tg 29° 12' 15"

c = (239 m)/0,5590

c = 427,47 m

e)

Aplicando el teorema de Pitágoras

a² = b² + c²

a² = (15 m)² + (7 m)²

a² = 225 m² + 49 m²

a² = 274 m²

a = 16,55 m

tg B = b/c

tg B = (15 m)/(7 m)

tg B = 2,1428

B = arctg 2,1428

B = 64° 58' 59"

tg C = c/b

tg C = (7 m)/(15 m)

tg C = 0,4667

C = arctg 0,4667

C = 25° 1' 1"

• ‹ Anterior
• |
• Regresar a la guía TP06
• |
• Siguiente ›

Autor: Ricardo Santiago Netto (Administrador de Fisicanet)

San Martín. Buenos Aires. Argentina.

Ver condiciones para uso de los contenidos de fisicanet.com.ar

• 🔍
• ✉ f t