Problema nº 8 de trigonometría, aplicar identidades trigonométricas - TP06

Enunciado del ejercicio nº 8

Verificar las siguientes identidades:

a) sen α - (tg α)·cos α = 0

b) sec² α·(cosec² α - 1) = cosec² α

c)

d) sen² α - sen² α·cos² β = (sen² β) - (sen² β)·(cos² α)

e) (1 + tg α)·(1 - tg α) = 2 - sec² α

Solución

a)

sen α - (sen α/cos α)·cos α = 0

sen α - sen α = 0

b)

Reemplazamos en el primer término:

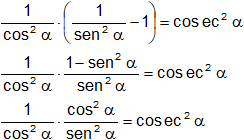
Simplificamos:

∎

c)

A = tg α·tg β·(cotg α + cotg β)

Reemplazamos en el primer término:

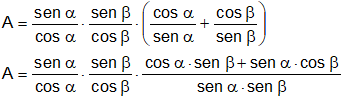
Simplificamos:

∎

d)

sen² α - sen² α·(1 - sen² β) = sen² β - sen² β·cos² α

sen² α - sen² α + (sen² α)·(sen² β) = sen² β - sen² β·cos² α

(sen² α)·(sen² β) = sen² β - sen² β·cos² α

(1 - sen² α)·sen² β = sen² β - sen² β·cos² α

sen² β - (sen² α)·(sen² β) = sen² β - sen² β·cos² α

e)

1 - tg² α = 2 - sec² α

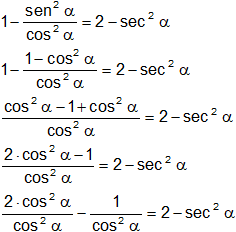
Simplificamos:

2 - sec² α = 2 - sec² α ∎

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP06
• | Siguiente ›

Ejemplo, cómo aplicar identidades trigonométricas