Ángulos entre dos vectores
• Nota: En éste trabajo las letras con una raya arriba representan un vector, por ejemplo ā es el vector a.
Ejemplo de cálculo del ángulo que forman dos vectores
Ejemplo nº 1
Dada la base del plano {ŭ₁, ŭ₂} donde |ŭ₁| = 2, |ŭ₂| = 1 y los vectores ŭ₁, ŭ₂ son perpendiculares, calcular el ángulo que forman los vectores ā = 3·ŭ₁ - 2·ŭ₂ y 
= 2·ŭ₁ + 5·ŭ₂
Solución
ŭ₁·ŭ₁ = |ŭ₁|² = 2² = 4
ŭ₁·ŭ₂ = ŭ₂·ŭ₁ = 0, ya que ambos vectores son perpendiculares, ŭ₂ = 6·4 + 15·0 - 4·0 - 10·1 = 14
De la misma forma:
ā·ā = (3·ŭ₁ - 2·ŭ₂)·(3·ŭ₁ - 2·ŭ₂) = 9·4 - 6·0 - 6·0 + 4·1 = 40
· = (2·ŭ₁ + 5·ŭ₂)·(2·ŭ₁ + 5·ŭ₂) = 4·4 + 10·0 + 10·0 + 25·1 = 41
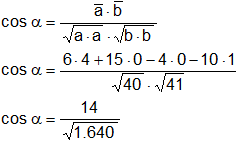
cos α = 0,34
α = arccos 0,34 = 69,8°
Bases ortonormales
Se dice que una base {ŭ₁, ŭ₂} es ortogonal si los dos vectores que la forman tienen módulo 1 y son perpendiculares entre sí.
Cuando se trabaja con este tipo de bases es sencillo calcular los productos escalares, ya que
ŭ₁·ŭ₁ = |ŭ₁| = 1, porque ŭ₁ tiene módulo 1·ŭ₂·ŭ₂ = |ŭ₂| = 1, por el mismo argumento.
ŭ₁·ŭ₂ = 0, por ser perpendiculares ambos vectores.
Aplicando estos resultados a las fórmulas ya obtenidas, se tiene que dados los vectores
= x₁·ŭ₁ + x₂·ŭ₂
= y₁·ŭ₁ + y₂·ŭ₂
· = x₁·y₁ + x₂·y₂
· = x₁² + x₂²
y siendo α el ángulo que forman,
Ejercicios con bases ortonormales
En todos los ejercicios siguientes se considera que {ŭ₁, ŭ₂} es una base ortogonal ortonormal del plano.
Ejercicio nº 1
Hallar la proyección del vector ā sobre el vector , siendo ā = 2·ŭ₁ + ŭ₂·y
= 3·ŭ₁ + 2·ŭ₂
Solución
En primer lugar se calcula el módulo de dicha proyección. Para ello es conveniente recordar que el producto escalar de dos vectores es igual al producto del módulo de uno de ellos por la proyección del otro sobre él.
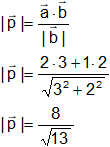
Para determinar la proyección se observa que, por ser ésta paralela al vector será de la forma.
= t·, donde t es un número real. Como el producto escalar es positivo, esto quiere decir que la proyección tiene el mismo sentido que , con lo que t ha de ser positivo.
Entonces, 
= |t·| = t·
, con lo que 
.
Sustituyendo:
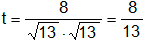
Así, = t· = (8/13)·(3·ŭ₁ + 2·ŭ₂) = (24/13)·ŭ₁ + (16/13)·ŭ₂
Ejercicio nº 2
Hallar el área de un paralelogramo cuyos lados no paralelos son los vectores
ā = 4·ŭ₁ - 3·ŭ₂ y = 2·ŭ₁ + 3·ŭ₂
Solución
El área de un paralelogramo es igual al producto de dos de sus lados por el seno del ángulo que forman:
S = ·h = |ā|··sen α, puesto que sen α = h/|ā|
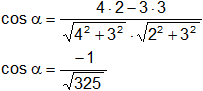
Para calcular el seno de este ángulo se aplica la fórmula fundamental de la trigonometría: sen² α + cos² α = 1 (relación pitagórica).
Así,
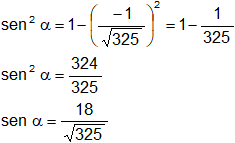
Y así el área es:
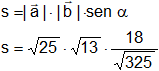
S = 18
Ejercicio nº 3
Aplicando la definición de producto escalar, demostrar el teorema de Pitágoras.
Solución
Sea un triángulo rectángulo, llamando y 
a los vectores que se pueden construir en los catetos y ā al vector de la hipotenusa, tal como se indica en la figura, se tiene ā = + , donde:
|ā|² = ā·ā = ( + )·( - ) = · + · + · + ·
Pero, por ser un triángulo rectángulo, resulta que · = · = 0.
Así:
|ā|² = · + · = ² + 
², que es la expresión del teorema de Pitágoras
Ejercicio nº 4
Demostrar que las dos diagonales de un rombo son perpendiculares.
Solución
Sean ā y dos lados consecutivos del rombo. Sus diagonales son ā + y ā - .
Para ver que son perpendiculares bastará con comprobar que su producto escalar es 0:
(ā + )·(ā - ) = ā·ā - ā· + ·ā - ·
Por la propiedad conmutativa del producto escalar, ā· = ·ā. Así pues,
(ā + )·(ā - ) = ā·ā - · = |ā|² - ²
Hasta ahora no se ha utilizado el hecho de que se está trabajando con un rombo.
Esto significa que los dos lados |ā| y son iguales. Entonces (ā + )·(ā - ) = |ā|² - ² = 0,
Con lo que las dos diagonales son perpendiculares.
Autor: Patricia Bati. Argentina.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
¿Qué es el producto vectorial entre vectores?