Problema nº 2 de ecuaciones de segundo grado o cuadráticas - TP01
Enunciado del ejercicio nº 2
Dada la ecuación 18·x² - 12·k·x + (6·k - 2) = 0, determinar el valor de "k" para que:
a) Sus raíces sean iguales.
b) Sus raíces sean opuestas.
c) Sus raíces sean recíprocas.
d) Una de sus raíces sea nula.
Desarrollo
Datos:
18·x² - 12·k·x + (6·k - 2) = 0
Fórmulas:
Ecuación de Báscara o Bhaskara:
Solución
Extraemos factor común "2":
2·[9·x² - 6·k·x + (3·k - 1)] = 0
9·x² - 6·k·x + (3·k - 1) = 0
Aplicamos la ecuación, siendo:
a = 9
b = -6·k
c = 3·k - 1
| x1,2 = | -(-6·k) ± √(-6·k)² - 4·9·(3·k - 1) |
| 2·9 |
| x1,2 = | 6·k ± √36·k² - 36·(3·k - 1) |
| 18 |
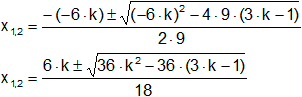
Extraemos factor común "36" dentro de la raíz:
| x1,2 = | 6·k ± √36·[k² - (3·k - 1)] |
| 18 |
Extraemos "6" de la raíz:
| x1,2 = | 6·k ± 6·√k² - 3·k + 1 |
| 18 |
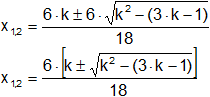
Simplificamos:
| x1,2 = | k ± √k² - 3·k + 1 | (1) |
| 3 |
Usaremos esta ecuación para los cálculos.
a)
Para que sus raíces sean iguales:
x₁ = x₂
Entonces, de la ecuación (1):
| k + √k² - 3·k + 1 | = | k - √k² - 3·k + 1 |
| 3 | 3 |
Simplificamos:
| k + √k² - 3·k + 1 | = | k - √k² - 3·k + 1 |
| 3 | 3 |
√k² - 3·k + 1 = -√k² - 3·k + 1
Igualamos a cero:
√k² - 3·k + 1 + √k² - 3·k + 1 = 0
2·√k² - 3·k + 1 = 0
√k² - 3·k + 1 = 0
k² - 3·k + 1 = 0
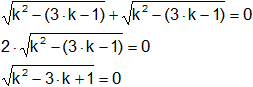
| k1,2 = | -b ± √b² - 4·a·c |
| 2·a |
Siendo:
a = 1
b = -3
c = 1
| k1,2 = | -(-3) ± √(-3)² - 4·1·1 |
| 2·1 |
| k1,2 = | 3 ± √9 - 4 |
| 2 |
| k1,2 = | 3 ± √5 |
| 2 |
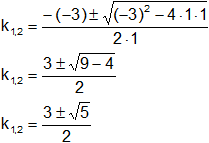
Obtenemos dos resultados para "k":
| k₁ = | 3 + √5 |
| 2 |
k₁ = 2,6180
| k₂ = | 3 - √5 |
| 2 |
k₂ = 0,3820
Aplicamos nuevamente la ecuación (1) con los resultados hallados de "k":
| x1,2 = | k ± √k² - 3·k + 1 |
| 3 |
Para k₁:
| x1,2 = | k₁ ± √k₁² - 3·k₁ + 1 |
| 3 |
| x1,2 = | 2,6180 ± √2,6180² - 3·2,6180 + 1 |
| 3 |
| x1,2 = | 2,6180 ± √6,8541 - 7,8541 + 1 |
| 3 |
| x1,2 = | 2,6180 ± √0 |
| 3 |
| x1,2 = | 2,6180 |
| 3 |
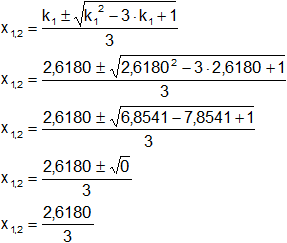
x1,2 = 0,8727
Para k₂:
| x3,4 = | k₂ ± √k₂² - 3·k₂ + 1 |
| 3 |
| x3,4 = | 0,3820 ± √0,3820² - 3·0,3820 + 1 |
| 3 |
| x3,4 = | 0,3820 ± √0,1459 - 1,1459 + 1 |
| 3 |
| x3,4 = | 0,3820 ± √0 |
| 3 |
| x3,4 = | 0,3820 |
| 3 |
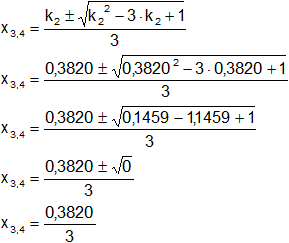
x3,4 = 0,1273
Resultado:
k₁ = 2,6180
k₂ = 0,3820
Para k₁, las raíces son:
x₁ = x₂ = 0,8727
Para k₂, las raíces son:
x₃ = x₄ = 0,1273
b)
Para que sus raíces sean opuestas:
x₁ + x₂ = 0
Entonces, de la ecuación (1):
| k + √k² - 3·k + 1 | = - | k - √k² - 3·k + 1 |
| 3 | 3 |
Simplificamos:
| k + √k² - 3·k + 1 | = | -k + √k² - 3·k + 1 |
| 3 | 3 |
k + √k² - 3·k + 1 = -k + √k² - 3·k + 1
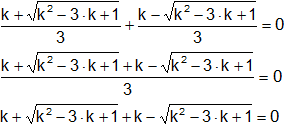
k = - k
2·k = 0
k = 0
Aplicamos nuevamente la ecuación (1) con el resultado hallado de "k":
| x1,2 = | k ± √k² - 3·k + 1 |
| 3 |
| x1,2 = | 0 ± √0² - 3·0 + 1 |
| 3 |
| x1,2 = | ± √1 |
| 3 |
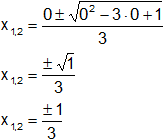
Resultado, el valor de "k" es:
k = 0
Las raíces son:
| x₁ = | 1 |
| 3 |
| x₂ = - | 1 |
| 3 |
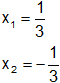
c)
Para que sus raíces sean recíprocas:
x₁·x₂ = 1
Entonces, de la ecuación (1):
| k + √k² - 3·k + 1 | = | 3 |
| 3 | k - √k² - 3·k + 1 |
(k + √k² - 3·k + 1)·(k - √k² - 3·k + 1) = 3·3
Resolvemos:
k² - (√k² - 3·k + 1)² = 9
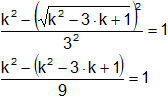
k² - k² + 3·k - 1 = 9
3·k - 1 = 9
Despejamos "k":
3·k = 9 + 1
3·k = 10
| k = | 10 |
| 3 |
Aplicamos nuevamente la ecuación (1) con el resultado hallado de "k":
| x1,2 = | k ± √k² - 3·k + 1 |
| 3 |
| x1,2 = | 10/3 ± √(10/3)² - 3·(10/3) + 1 |
| 3 |
| x1,2 = | 10/3 ± √100/9 - 10 + 1 |
| 3 |
| x1,2 = | 10/3 ± √100/9 - 9 |
| 3 |
| x1,2 = | 10/3 ± √(100 - 81)/9 |
| 3 |
| x1,2 = | 10/3 ± √19/9 |
| 3 |
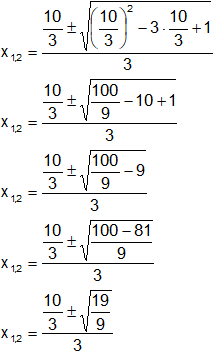
Extraemos "⅑" de la raíz:
| x1,2 = | 10/3 ± ⅓·√19 |
| 3 |
| x1,2 = | 10 ± √19 |
| 9 |
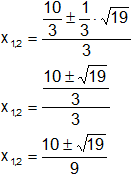
Resultado, el valor de "k" es:
| k = | 10 |
| 3 |
Las raíces son:
| x₁ = | 10 + √19 |
| 9 |
| x₂ = | 10 - √19 |
| 9 |
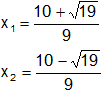
d)
Para que una de sus raíces sea nula:
x₁ = 0 ∨ x₂ = 0
Entonces, de la ecuación (1):
| x₁ = | k₁ + √k₁² - 3·k₁ + 1 | = 0 |
| 3 |
∨
| x₂ = | k₂ - √k₂² - 3·k₂ + 1 | = 0 |
| 3 |
Calculamos para x₁:
| k₁ + √k₁² - 3·k₁ + 1 | = 0 |
| 3 |
k₁ + √k₁² - 3·k₁ + 1 = 0
k₁ = -√k₁² - 3·k₁ + 1
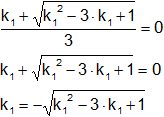
Elevamos ambos términos al cuadrado para eliminar la raíz:
k₁² = (-√k₁² - 3·k₁ + 1)²
Cancelamos:
k₁² = k₁² - 3·k₁ + 1
Despejamos k₁:
0 = -3·k₁ + 1
3·k₁ = 1
| k₁ = | 1 |
| 3 |
Calculamos para x₂:
| k₂ - √k₂² - 3·k₂ + 1 | = 0 |
| 3 |
k₂ - √k₂² - 3·k₂ + 1 = 0
k₂ = √k₂² - 3·k₂ + 1
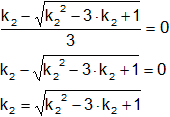
Elevamos ambos términos al cuadrado para eliminar la raíz:
k₂² = (√k₂² - 3·k₂ + 1)²
Cancelamos:
k₂² = k₂² - 3·k₂ + 1
Despejamos k₂:
0 = -3·k₂ + 1
3·k₂ = 1
| k₂ = | 1 |
| 3 |
Aplicamos nuevamente la ecuación (1) con el resultado hallado de "k":
| x1,2 = | k ± √k² - 3·k + 1 |
| 3 |
| k₁ = k₂ = | 1 |
| 3 |
| x1,2 = | ⅓ ± √⅓² - 3·⅓ + 1 |
| 3 |
| x1,2 = | ⅓ ± √⅓² - 1 + 1 |
| 3 |
| x1,2 = | ⅓ ± √⅓² |
| 3 |
| x1,2 = | ⅓ ± ⅓ |
| 3 |
| x1,2 = | 1 ± 1 |
| 9 |
| x₁ = | 1 + 1 |
| 9 |
| x₂ = | 1 - 1 |
| 9 |
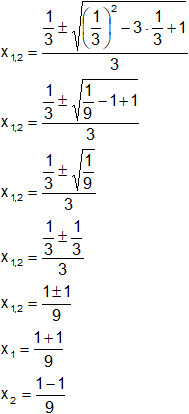
Resultado, el valor de "k" es:
| k = | 1 |
| 3 |
Las raíces son:
| x₁ = | 2 |
| 9 |
x₂ = 0
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP01
- | Siguiente ›
Ejemplo, cómo resolver ecuaciones cuadraticas