Guía nº 1 de ejercicios resueltos de ecuaciones de segundo grado
Resolver los siguientes ejercicios
� Ver resolución de los ejercicios al pie de la página
Problema nº 1
¿Cuál debe ser el valor del coeficiente "a", si se sabe que el valor de la función y = a·x² para x = 1 es igual a 2?
• Respuesta: a = 2
Problema nº 2
Dada la ecuación 18·x² - 12·k·x + (6·k - 2) = 0, determinar el valor de "k" para que:
a) Sus raíces sean iguales.
b) Sus raíces sean opuestas.
c) Sus raíces sean recíprocas.
d) Una de sus raíces sea nula.
• Respuesta:
a) k₁ = 2,6180 y k₂ = 0,3820;
b) k = 0;
c) k = 10/3;
d) k = ⅓
Problema nº 3
Factorear:
a) y = 2·x² - x - 1
b) y = 5·x² + 3·x - 2
c) y = x² - 2·x + 1
d) y = 4·x² + 16·x + 15
• Respuesta:
a) y = (x - 1)·(x + ½);
b) y = (x + 1)·(x - ⅖);
c) y = (x - 1)²;
d) ![]()
Problema nº 4
Obtener las ecuaciones cuyas raíces son:
a) x₁ = ⅓ ∧ x₂ = -3/2
b) x₁ = -½ + 2·i ∧ x₂ = -½ - 2·i
c) x₁ = 0 ∧ x₂ = -4/3
• Respuesta:
a) ![]()
b) ![]()
c) ![]()
Problema nº 5
Resolver los siguientes sistemas:
a)
![]()
b)
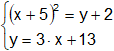
• Respuesta:
a) P₁(1; 5) y P₂(-2; -4);
b) P₁(-2; 7) y P₂(-5; -2)
Problema nº 6
Calcular el valor de la constante "p" de modo que la suma de las raíces de la ecuación:
(2·p - 1)·x² + (p + 2)·x - 7·p = 0
Sea igual a - 4/3
• Respuesta: p = 2
Autor: Ricardo Santiago Netto. Argentina