Problema nº 4 de ecuaciones de segundo grado, generar ecuaciones cuadráticas partiendo de sus raíces - TP01

Enunciado del ejercicio nº 4

Obtener las ecuaciones cuyas raíces son:

a) x₁ = ⅓ ∧ x₂ = -3/2

b) x₁ = -½ + 2·i ∧ x₂ = -½ - 2·i

c) x₁ = 0 ∧ x₂ = -4/3

Solución

a)

x₁ = ⅓ ∧ x₂ = -3/2

Armamos la ecuación en forma de producto de binomios:

y = (x - x₁)·(x - x₂)

Reemplazamos por las raíces cuidando los signos:

Desarrollamos el producto:

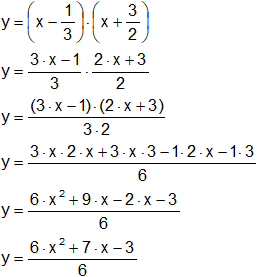
Distribuimos el denominador:

Simplificamos:

Expresamos el resultado:

b)

x₁ = -½ + 2·i ∧ x₂ = -½ - 2·i

En este caso tenemos raíces complejas. Armamos la ecuación en forma de producto de binomios:

y = (x - x₁)·(x - x₂)

Reemplazamos por las raíces cuidando los signos:

y = [x - (-½ + 2·i)]·[x - (-½ - 2·i)]

Desarrollamos el producto:

y = (x + ½ - 2·i)·(x + ½ + 2·i)

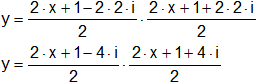
Agrupamos para aplicar diferencia de cuadrados:

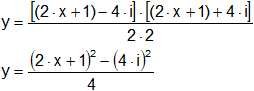
De esta forma eliminamos fácilmente la parte imaginaria del complejo.

i² = -1

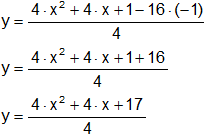
Distribuimos el denominador:

Simplificamos:

Expresamos el resultado:

c)

x₁ = 0 ∧ x₂ = -4/3

Armamos la ecuación en forma de producto de binomios:

y = (x - x₁)·(x - x₂)

Reemplazamos por las raíces cuidando los signos:

Desarrollamos el producto:

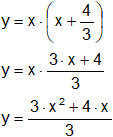
Distribuimos el denominador:

Simplificamos:

Expresamos el resultado:

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP01
• | Siguiente ›

Ejemplo, cómo generar ecuaciones cuadraticas partiendo de sus raíces