Problema nº 6 de ecuaciones de segundo grado o cuadráticas - TP01
Enunciado del ejercicio nº 6
Calcular el valor de la constante "p" de modo que la suma de las raíces de la ecuación:
(2·p - 1)·x² + (p + 2)·x - 7·p = 0
Sea igual a ![]()
Solución
Pide:
x₁ + x₂ = -4/3
Aplicamos la ecuación de Báscara o Bhaskara:
![]()
Siendo:
a = 2·p - 1
b = p + 2
c = -7·p
Reemplazamos y desarrollamos:
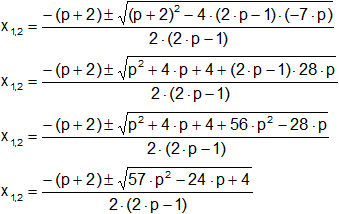
Desglosamos la ecuación
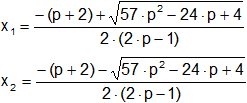
La condición es: x₁ + x₂ = ![]()
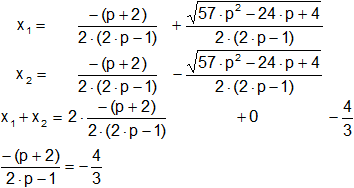
Resolvemos:
-(p + 2)·3 = -4·(2·p - 1)
3·p + 4 = 8·p - 4
Despejamos "p":
3·p - 8·p = -4 - 6
-5·p = -10
p = 2
Resultado, el valor de la constante "p" es:
p = 2
Expresamos la ecuación buscada:
(2·p - 1)·x² + (p + 2)·x - 7·p = 0
(2·2 - 1)·x² + (2 + 2)·x - 7·2 = 0
(4 - 1)·x² + 4·x - 14 = 0
3·x² + 4·x - 14 = 0
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP01
- | Siguiente ›
Ejemplo, cómo resolver ecuaciones cuadraticas