Problema nº 18 de ecuaciones de primer grado, despejar "x" - TP02

Enunciado del ejercicio nº 18

Resolver la siguiente ecuación hallando el valor de "x":

Solución

Observando los denominadores del primer miembro y del cuarto miembro notamos que son polinomios divisibles por "x - 1", ya que haciendo x = 1 dichos polinomios se anulan. Dividimos:

(x³ - x² + x - 1)÷(x - 1) =

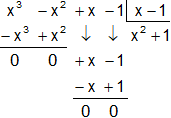
x³	- x²	+ x	- 1	x - 1
- x³	+ x²	↓	↓	x² + 1
0	0	+ x	- 1
		- x	+ 1
R =		0	0

(x³ - x² + x - 1) = (x - 1)·(x² + 1)

(x³ - x² - x + 1)÷(x - 1) =

x³	- x²	- x	+ 1	x - 1
- x³	+ x²	↓	↓	x² - 1
0	0	- x	+ 1
		+ x	- 1
R =		0	0

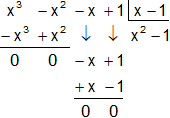
(x³ - x² - x + 1) = (x - 1)·(x² - 1)

Reemplazamos:

El tercer miembro es una diferencia de potencias de igual grado par, la factorizamos:

Factorizamos las diferencias de cuadrados:

Igualamos a cero:

Sumamos las fracciones, el denominador común será "(x - 1)²·(x + 1)·(x² + 1)":

Pasamos el denominador del otro lado del signo "=" multiplicando:

2·(x - 1)·(x + 1) - 1·(x - 1)²·(x + 1) + x²·(x - 1) - 2·(x² + 1) = 0·(x - 1)²·(x + 1)·(x² + 1)

2·(x² - 1) - (x - 1)²·(x + 1) + x²·(x - 1) - 2·(x² + 1) = 0

Desarrollamos el binomio al cuadrado y aplicamos distributiva del producto respecto a la suma y la resta:

2·x² - 2·1 - (x² - 2·x·1 + 1²)·(x + 1) + x²·x - x²·1 - (2·x² + 2·1) = 0

Sumamos los términos de igual grado:

2·x² - 2 - (x² - 2·x + 1)·(x + 1) + x³ - x² - 2·x² - 2 = 0

-(x²·x - 2·x·x + 1·x + x²·1 - 2·x·1 + 1·1) + x³ - x² - 4 = 0

-(x³ - 2·x² + x + x² - 2·x + 1) + x³ - x² - 4 = 0

-(x³ - x² - x + 1) + x³ - x² - 4 = 0

-x³ + x² + x - 1 + x³ - x² - 4 = 0

x - 5 = 0

Despejamos "x" y tenemos el resultado:

x = 5

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo, cómo resolver ecuaciones de primer grado. Despejar "x".