Problema nº 1-d de ecuaciones de segundo grado o cuadráticas, raíces - TP04

Enunciado del ejercicio nº 1-d

Hallar las raíces. ¿Para qué valores de "x" la ecuación es igual a cero?

Ecuación de Báscara o Bhaskara:

Sumamos las fracciones, el denominador común será "(x - 5)·(x - 2)":

En el denominador aplicamos distributiva del producto respecto a la resta:

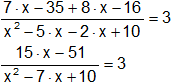
Resolución de ecuaciones cuadráticas

Pasamos el denominador del otro lado del signo "=" multiplicando:

15·x - 51 = 3·(x² - 7·x + 10)

15·x - 51 = 3·x² - 21·x + 30

Expresamos la ecuación en forma implícita y ordenada.

3·x² - 21·x + 30 - 15·x + 51 = 0

3·x² - 36·x + 81 = 0

Extraemos factor común 3:

3·(x² - 12·x + 27) = 0

x² - 12·x + 27 = 0

Aplicamos la ecuación de Báscara o Bhaskara, siendo:

a = 1

b = -12

c = 27

Reemplazamos y resolvemos, obtendremos dos valores:

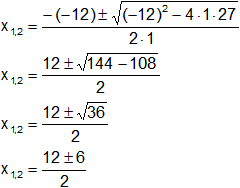
Cálculo de raíces

x_1,2 = 6 ± 3

Calculamos los valores por separado según el signo del resultado de la raíz:

x₁ = 6 + 3

x₁ = 9

x₂ = 6 - 3

x₂ = 3

Resultado, las raíces son:

x₁ = 9

x₂ = 3

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo, cómo hallar las raíces en ecuaciones cuadráticas