Guía nº 4 de ejercicios resueltos de ecuaciones
Resolver los siguientes ejercicios
� Ver resolución de los ejercicios al pie de la página
Problema nº 1
Hallar las raíces. ¿Para qué valores de "x" las siguientes ecuaciones son iguales a cero?
a) x² = 3·x + 18
• Respuesta: x₁ = 6, x₂ = -3
b) x⁴ + 36 = 13·x²
• Respuesta: x₁ = 3, x₂ = -3, x₃ = 2, x₄ = -2
c) ![]()
• Respuesta: x1,2 ∉ ℜ
d) ![]()
• Respuesta: x₁ = 9, x₂ = 3
e) ![]()
• Respuesta: x₁ = 3, x₂ = 1
f) (x² - 1)² + 3 = 4·(x + 1)·(x - 1)
• Respuesta: x₁ = 0, x₂ = 3
g) ![]()
• Respuesta: x₁ = 8, x₂ = -5
h) ![]()
• Respuesta: x₁ = 3/2, x₂ = 5/8
Problema nº 2
Hallar los valores de "x" para los cuales las siguientes ecuaciones son iguales a cero.
a) 3·x³ = 65·x + 2·x²
• Respuesta: x₁ = 6, x₂ = -3
b) 0,1·x³ + 0,35·x² + 0,8·x = x
• Respuesta: x₁ = 3, x₂ = -3, x₃ = 2, x₄ = -2
c) 0,09·x⁴ + 0,1·x² = 0,21·x³
• Respuesta: x1,2 ∉ ℜ
d) x²·(x - 6)·(x - 5) + (x - 7)·(x - 4)·x² = 2·x²
• Respuesta: x₁ = 9, x₂ = 3
e) ![]()
• Respuesta: x₁ = 0, x₂ = 5
f) ![]()
• Respuesta: x₁ = 2, x₂ = -2, x₃ = ![]() , x₄ = -
, x₄ = -![]()
g) ![]()
• Respuesta: x₁ = 1, x₂ = -1, x₃ = ⅓, x₄ = -⅓
h) ![]()
• Respuesta:
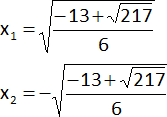
x3,4 ∉ ℜ
Problema nº 3
Obtener las ecuaciones cuyas raíces son:
a) ![]()
• Respuesta: x² - 4·x - 2 = 0
b) ![]()
• Respuesta: ![]()
c) x₁ = 0; x₂ = -3 ∧ x₃ = -8
• Respuesta: x³ + 11·x² + 24·x = 0
d) x₁ = 1; x₂ = x₃ = 0 ∧ x₄ = -7/2
• Respuesta: ![]()
e) x₁ = -x₂ = 0,2 ∧ x₃ = -x₄ = -0,5·i
• Respuesta: x⁴ + 0,21·x² - 0,01 = 0
Autor: Ricardo Santiago Netto. Argentina