Problema nº 3-b, generar ecuaciones de segundo grado o cuadráticas dadas las raíces - TP04

Enunciado del ejercicio nº 3-b

Obtener la ecuación cuyas raíces son:

Solución

Dadas las raíces la ecuación se obtiene planteando el producto de binomios de primer grado, este producto se iguala a cero, un binomio por cada raíz, luego se desarrollan los productos.

Planteamos el producto, dos binomios:

(x - x₁)·(x - x₂) = 0

Reemplazamos por las raíces:

Resolvemos:

Aplicamos la inversa de la diferencia de cuadrados:

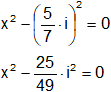
i² = -1

Resultado, la ecuación es:

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP04
• | Siguiente ›

Ejemplo, cómo hallar ecuaciones dadas las raíces