Problema nº 2-k y 2-l, hallar las raíces en ecuaciones irracionales de segundo grado - TP17
Enunciado del ejercicio nº 2-k y 2-l
Resolver las siguientes ecuaciones irracionales de segundo grado:
k) ![]()
l) ![]()
Solución
k)
![]()
Despejamos las raíces:
![]()
Elevamos ambos miembros al cuadrado, con esto iremos cancelando raíces cuadradas:
![]()
Resolvemos el binomio al cuadrado:
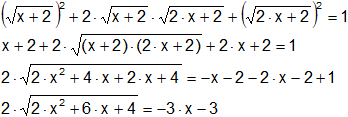
Elevamos ambos miembros al cuadrado para cancelar la raíz cuadrada:
![]()
Resolvemos:
4·(2·x² + 6·x + 4) = 9·x² + 18·x + 9
8·x² + 24·x + 16 = 9·x² + 18·x + 9
Igualamos a cero para obtener la ecuación implícita:
8·x² + 24·x + 16 - 9·x² - 18·x - 9 = 0
Agrupamos y sumamos los términos según las potencias de "x":
8·x² - 9·x² + 24·x - 18·x + 16 - 9 = 0
-x² + 6·x + 7 = 0
x² - 6·x - 7 = 0
Tenemos la ecuación planteada en forma implícita, completa y ordenada.
Aplicamos la ecuación de Báscara o Bhaskara:
![]()
Siendo:
a = 1
b = -6
c = -7
Reemplazamos y resolvemos, obtendremos dos valores:
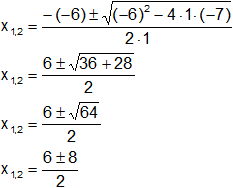
x1,2 = 3 ± 4
Calculamos los valores por separado según el signo del resultado de la raíz:
x₁ = 3 + 4
x₁ = 7
x₂ = 3 - 4
x₂ = -1
Expresamos el resultado.
La ecuación expresada en forma implícita es:
x² - 6·x - 7 = 0
Las raíces son:
x₁ = 7
x₂ = -1
l)
![]()
Elevamos ambos miembros al cuadrado para comenzar a cancelar la raíces cuadradas:
![]()
Resolvemos:
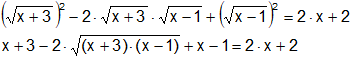
Despejamos la raíz:
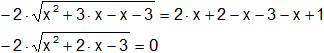
Elevamos ambos miembros al cuadrado para cancelar la raíz cuadrada:
![]()
Resolvemos:
x² + 2·x - 3 = 0
Tenemos la ecuación planteada en forma implícita, completa y ordenada.
Aplicamos la ecuación de Báscara o Bhaskara:
![]()
Siendo:
a = 1
b = 2
c = -3
Reemplazamos y resolvemos, obtendremos dos valores:
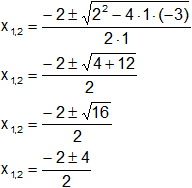
x1,2 = -1 ± 2
Calculamos los valores por separado según el signo del resultado de la raíz:
x₁ = -1 + 2
x₁ = 1
x₂ = -1 - 2
x₂ = -3
Expresamos el resultado.
La ecuación expresada en forma implícita es:
x² + 2·x - 3 = 0
Las raíces son:
x₁ = 1
x₂ = -3
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP17
- | Siguiente ›
Ejemplo, cómo hallar las raíces en ecuaciones irracionales de segundo grado