Problema nº 3-c de funciones cuadráticas o de segundo grado - TP02
Enunciado del ejercicio nº 3-c
Hallar las intersecciones con los ejes, el vértice y graficar la siguiente función:
x² - 4·x - 2·y + 4 = 0
Solución
x² - 4·x - 2·y + 4 = 0
Despejamos "y", expresamos la función en forma explícita:
2·y = x² - 4·x + 4
| y = | x² | - 2·x + 2 |
| 2 |
Hallamos la intersección con el eje "X" para y = 0, hallamos las raíces:
| x² | - 2·x + 2 = 0 |
| 2 |
Aplicamos la ecuación de Báscara o Bhaskara:
| x1,2 = | -b ± √b² - 4·a·c |
| 2·a |
Siendo:
a = ½
b = -2
c = 2
Reemplazamos y resolvemos, obtendremos dos valores:
| x1,2 = | -(-2) ± √(-2)² - 4·½·2 |
| 2·½ |
| x1,2 = | 2 ± √4 - 4 |
| 1 |
x1,2 = 2 ± √0
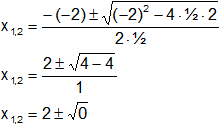
x1,2 = 2
La intersección con el eje "X" es:
x1,2 = 2
Hallamos la intersección con el eje "Y" para x = 0:
| y = | x² | - 2·x + 2 |
| 2 |
| y = | 0² | - 2·0 + 2 |
| 2 |
y = 2
La intersección con el eje "Y" es:
y = 2
El vértice en "X" de la parábola es el punto medio de sus raíces:
| Vₓ = | x₂ + x₁ |
| 2 |
Reemplazamos por los valores y calculamos:
| Vₓ = | 2 + 2 |
| 2 |
| Vₓ = | 4 |
| 2 |
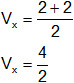
Vₓ = 2
El vértice en "Y" de la parábola se calcula reemplazando a "x" por "Vₓ":
| Vy = | Vₓ² | - 2·Vₓ + 2 |
| 2 |
| Vy = | 2² | - 2·2 + 2 |
| 2 |
| Vy = | 4 | - 4 + 2 |
| 2 |
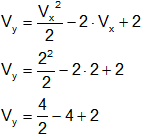
Vy = 2 - 2
Vy = 0
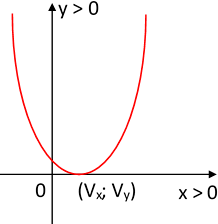
El vértice es:
V = (Vₓ; Vy)
V = (2; 0)
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP02
- | Siguiente ›
Ejemplo, cómo resolver funciones cuadráticas