Problema nº 7-a de funciones logarítmicas, operaciones con logaritmos - TP04

Enunciado del ejercicio nº 7-a

Resolver la siguiente ecuación:

log₂ (x² + 1) - log₂ x = 1

log₂ (x² + 1) - log₂ x = 1

Aplicamos la propiedad inversa del logaritmo de un producto:

log₂	x² + 1	= 1
	x

Por definición de logaritmo:

logₐ n = x ⇔ aˣ = n

log₂	x² + 1	= 1 ⇔ 2¹ =	x² + 1
	x		x

2 =	x² + 1
	x

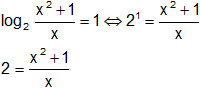
2·x = x² + 1

Igualamos a cero:

x² - 2·x + 1 = 0

Es un trinomio cuadrado perfecto:

x² - 2·x + 1 = (x - 1)²

Las raíces son:

x_1,2 = 1

Verificamos reemplazando los valores de "x" en la ecuación dada:

log₂ (x² + 1) - log₂ x = 1

log₂ (1² + 1) - log₂ 1 = 1

log₂ 2 - log₂ 1 = 1

1 - 0 = 1 ∎

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo, operaciones con logaritmos