Guía nº 4 de problemas resueltos de funciones logarítmicas
Resolver los siguientes ejercicios
� Ver resolución de los ejercicios al pie de la página
Problema nº 1
¿Cuál es la expresión "S" cuyo logaritmo decimal es: log 4 + log π + log r²?
• Respuesta: S = 4·π·r²
Problema nº 2
Si la suma de los logaritmos de dos números, en base 9, es ½, determinar el producto de esos números.
• Respuesta: a·b = ±3
Problema nº 3
Sabiendo que el log₂ (a - b) = m, y (a + b) = 8, obtener el log₂ (a² - b²) en función de m.
• Respuesta: log₂ (a² - b²) = m + 3
Problema nº 4
Resolver la ecuación:
log₂ (x - 3) + log₂ (x - 2) = 1.
• Respuesta: x₁ = 4; x₂ = 1 no es solución
Problema nº 5
Si la diferencia de logaritmos, en base 4, de dos números "x" e "y", en este orden, es ½, ¿qué relación existe entre "x" e "y"?
• Respuesta: x÷y = ±2
Problema nº 6
Reducir a logaritmo único:
log V = log 4 + log π + log r³ - log 3.
• Respuesta:
![]()
Problema nº 7
Resolver las siguientes ecuaciones:
a) log₂ (x² + 1) - log₂ x = 1
b) log₂ (9·x² - 20) - log₂ x - log₂ 6 = 2
c) log₄ x - log₄ (x - 1) = 1
d) log₄ x - log₂ x = 9
e) ![]()
f) ![]()
g) ![]()
• Respuesta:
a) x1,2 = 1
b)
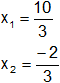
c)
![]()
d) x = 3,814·10⁻⁶
e) ![]() ;
;
f) x = 5
g) x = 2⁵
Problema nº 8
Aplicar logaritmo a:
![]()
• Respuesta: log S = ½·log 3 - 2·log 2
Problema nº 9
Reducir a logaritmo único:
a) log S = ½·[log p + log (p - a) +
+ log (p - b) + log (p - c)]
b) log X = ⅔·[log (a + b) +
+ log (a - b) - 1]
• Respuesta:
a) log S = log [p·(p - a)·(p - b)·(p - c)]½;
b) log X = log (a² - b²)⅔
Problema nº 10
Cambiar a base 10:
x = log₂ 10
• Respuesta:
![]()
Autor: Ricardo Santiago Netto. Argentina