Problema nº 12 de funciones de varias variables, longitud de una curva aplicando integrales - TP01
Enunciado del ejercicio nº 12
Calcular la longitud de la curva (t², t³); -2 ≤ t ≤ 1
Desarrollo
Fórmulas:
| s = ∫ | t₂ | ||X'(t)||·dt |
| t₁ |
| s = ∫ | b | √1 + [f'(x)]²·dx |
| a |
Solución
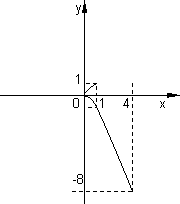
| t | t² | t³ |
| -2 | 4 | -8 |
| -1 | 1 | -1 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
La curva esta dada en forma paramétrica:
C(t) = (t², t³)
C'(t) = (2·t, 3·t²)
Su norma será:
||C'(t)|| = √(2·t)² + (3·t²)²
||C'(t)|| = √4·t² + 9·t⁴
||C'(t)|| = t·√4 + 9·t²
Planteamos la integral correspondiente entre los límites indicados:
| s = ∫ | t₂ | ||X'(t)||·dt |
| t₁ |
| s = ∫ | 1 | t·√4 + 9·t²·dt |
| -2 |
| s = -∫ | 0 | t·√4 + 9·t²·dt | +∫ | 1 | t·√4 + 9·t²·dt |
| -2 | 0 |
Por sustitución:
u = 4 + 9·t²
du = 18·t·dt
s = (1/18)·∫ √u·du
| s = | 1 | · | u3/2 |
| 18 | 3/2 |
s = (1/18)·⅔·√u³
s = (1/27)·√u³
Retomando:
| s = -(1/27)·√(4 + 9·t²)³·dt | 0 | + (1/27)·√(4 + 9·t²)³·dt | 1 |
| -2 | 0 |
| s = - | 1 | ·[√(4 + 9·(0)²)³] - [√(4 + 9·(-2)²)³] + | 1 | ·[√(4 + 9·(1)²)³] - [√(4 + 9·(0)²)³] |
| 27 | 27 |
| s = - | 1 | ·[√4³ - √(4 + 9·4)³] + | 1 | ·[√(4 + 9)³ - √4³] |
| 27 | 27 |
| s = - | 1 | ·(√4³ - √40³) + | 1 | ·(√13³ - √4³) |
| 27 | 27 |
| s = - | 8·√2 | + | 80·√10 | + | 13·√13 | - | 8·√2 |
| 27 | 27 | 27 | 27 |
| s = | 80·√10 - 16·√2 + 13·√13 |
| 27 |
Resultado, la longitud de la curva es:
s ≈ 10,27
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP01
- | Siguiente ›
Ejemplo, cómo hallar la longitud de una curva aplicando integrales