Problema nº 1 de graficar polinomios - TP10
Enunciado del ejercicio nº 1
Para cada uno de los siguientes polinomios completar la tabla y representar graficamente:
a)
P(x) = 3·x - 1
| x | -1 | 0 | ⅓ | 1 | 2 | 3 |
| P(x) = |
b)
P(x) = 2·x² - 1
| x | -1 | 0 | ½ | 1 | 1,5 | 2 |
| P(x) = |
c)
P(x) = x³ + 1
| x | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 |
| P(x) = |
Solución
a)
P(x) = 3·x - 1
Calculamos el valor numérico de P(x) para cada valor:
P(-1) = 3·(-1) - 1 ⇒ P(-1) = -3 - 1 ⇒ P(-1) = -4
P(0) = 3·0 - 1 ⇒ P(0) = 0 - 1 ⇒ P(0) = -1
P(⅓) = 3·⅓ - 1 ⇒ P(⅓) = 1 - 1 ⇒ P(⅓) = 0
P(1) = 3·1 - 1 ⇒ P(1) = 3 - 1 ⇒ P(1) = 2
P(2) = 3·2 - 1 ⇒ P(2) = 6 - 1 ⇒ P(2) = 5
P(3) = 3·3 - 1 ⇒ P(3) = 9 - 1 ⇒ P(3) = 8
Volcamos los datos en la tabla:
| x | -1 | 0 | ⅓ | 1 | 2 | 3 |
| P(x) = | -4 | -1 | 0 | 2 | 5 | 8 |
Graficamos la tabla de datos:
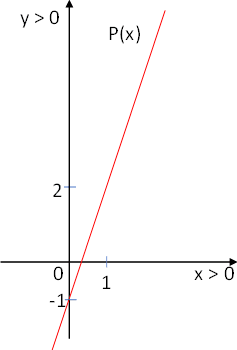
b)
P(x) = 2·x² - 1
Calculamos el valor numérico de P(x) para cada valor:
P(-1) = 2·(-1)² - 1 ⇒ P(-1) = 2·1 - 1 ⇒ P(-1) = 2 - 1 ⇒ P(-1) = 1
P(0) = 2·0² - 1 ⇒ P(0) = 2·0 - 1 ⇒ P(0) = 0 - 1 ⇒ P(0) = -1
P(½) = 2·(½)² - 1 ⇒ P(½) = 2·¼ - 1 ⇒ P(½) = ½ - 1 ⇒ P(½) = -½
P(1) = 2·1² - 1 ⇒ P(1) = 2·1 - 1 ⇒ P(1) = 1
P(1,5) = 2·1,5² - 1 ⇒ P(1,5) = 2·2,25 - 1 ⇒ P(1,5) = 4,5 - 1 ⇒ P(1,5) = 3,5
P(2) = 2·2² - 1 ⇒ P(2) = 2·4 - 1 ⇒ P(2) = 8 - 1 ⇒ P(2) = 7
Volcamos los datos en la tabla:
| x | -1 | 0 | ½ | 1 | 1,5 | 2 |
| P(x) = | 1 | -1 | -½ | 1 | 3,5 | 7 |
Graficamos la tabla de datos:
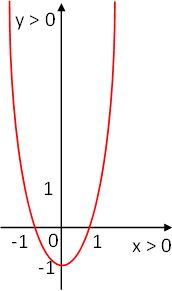
c)
P(x) = x³ + 1
Calculamos el valor numérico de P(x) para cada valor:
P(-1) = (-1)³ + 1 ⇒ P(-1) = -1 + 1 ⇒ P(-1) = 0
P(-0,5) = (-0,5)³ + 1 ⇒ P(-0,5) = -0,125 + 1 ⇒ P(-0,5) = 0,875
P(0) = 0³ + 1 ⇒ P(0) = 0 + 1 ⇒ P(0) = 1
P(0,5) = 0,5³ + 1 ⇒ P(0,5) = 0,125 + 1 ⇒ P(0,5) = 1,125
P(1) = 1³ + 1 ⇒ P(1) = 1 + 1 ⇒ P(1) = 2
P(1,5) = 1,5³ + 1 ⇒ P(1,5) = 3,375 + 1 ⇒ P(1,5) = 4,375
P(2) = 2³ + 1 ⇒ P(2) = 8 + 1 ⇒ P(2) = 9
Volcamos los datos en la tabla:
| x | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 |
| P(x) = | 0 | 0,875 | 1 | 1,125 | 2 | 4,375 | 9 |
Graficamos la tabla de datos:
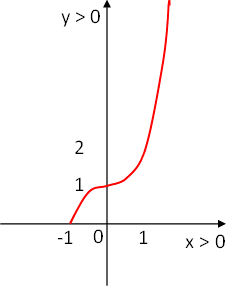
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP10
- | Siguiente ›
Ejemplo, cómo graficar polinomios