Problema nº 2 de cálculo de las raíces de un polinomio - TP11
Enunciado del ejercicio nº 2
Hallar las restantes raíces de los siguientes polinomios y factorizarlos:
a) x³ + x² - 14·x - 24, sabiendo que: -3 es raíz.
b) x⁴ + 3·x³ - 3·x² - 11·x - 6, sabiendo que: -1 es raíz doble.
Solución
a)
P(x) = x³ + x² - 14·x - 24
x₁ = -3
Si una de sus raíces es "-3" entonces el polinomio es divisible por "-3", aplicamos la regla de Ruffini:
| 1 | 1 | -14 | -24 | |
| -3 | -3 | 6 | 24 | |
| 1 | -2 | -8 | 0 | |
C(x) = x² - 2·x - 8
R = 0
P(x) = (x + 3)·(x² - 2·x - 8)
Hallamos las raíces para C(x), aplicamos la ecuación de Báscara o Bhaskara:
| x2,3 = | -b ± √b² - 4·a·c |
| 2·a |
Siendo:
a = 1
b = -2
c = -8
Reemplazamos y resolvemos, obtendremos dos valores:
| x2,3 = | -(-2) ± √(-2)² - 4·1·(-8) |
| 2·1 |
| x2,3 = | 2 ± √4 + 32 |
| 2 |
| x2,3 = | 2 ± √36 |
| 2 |
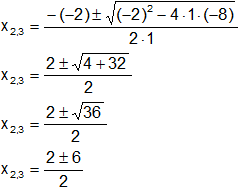
| x2,3 = | 2 ± 6 |
| 2 |
Calculamos los valores por separado según el signo del resultado de la raíz:
| x₂ = | 2 + 6 |
| 2 |
| x₂ = | 8 |
| 2 |
x₂ = 4
| x₃ = | 2 - 6 |
| 2 |
| x₃ = | -4 |
| 2 |
x₃ = -2
Resultado, las raíces del polinomio son:
x₁ = -3
x₂ = 4
x₃ = -2
El polinomio factorizado es:
x³ + x² - 14·x - 24 = (x + 3)·(x - 4)·(x + 2)
b)
P(x) = x⁴ + 3·x³ - 3·x² - 11·x - 6
x1,2 = -1
Si dos de sus raíces son "-1" entonces el polinomio es dos veces divisible por "-1", aplicamos la regla de Ruffini:
| 1 | 3 | -3 | -11 | -6 | |
| -1 | -1 | -2 | 5 | 6 | |
| 1 | 2 | -5 | -6 | 0 | |
C(x) = x³ + 2·x² - 5·x - 6
R = 0
P(x) = (x + 1)·(x³ + 2·x² - 5·x - 6)
Dividimos C(x) aplicando la regla de Ruffini:
| 1 | 2 | -5 | -6 | |
| -1 | -1 | -1 | 6 | |
| 1 | 1 | -6 | 0 | |
D(x) = x² + x - 6
R = 0
P(x) = (x + 1)²·(x² + x - 6)
Hallamos las raíces para D(x), aplicamos la ecuación de Báscara o Bhaskara:
| x3,4 = | -b ± √b² - 4·a·c |
| 2·a |
Siendo:
a = 1
b = 1
c = -6
Reemplazamos y resolvemos, obtendremos dos valores:
| x3,4 = | -1 ± √1² - 4·1·(-6) |
| 2·1 |
| x3,4 = | -1 ± √1 + 24 |
| 2 |
| x3,4 = | -1 ± √25 |
| 2 |
| x3,4 = | -1 ± 5 |
| 2 |
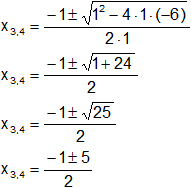
Calculamos los valores por separado según el signo del resultado de la raíz:
| x₃ = | -1 + 5 |
| 2 |
| x₃ = | 4 |
| 2 |
x₃ = 2
| x₄ = | -1 - 5 |
| 2 |
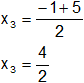
| x₄ = | -6 |
| 2 |
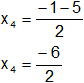
x₄ = -3
Resultado, las raíces del polinomio son:
x1,2 = -1
x₃ = 2
x₄ = -3
El polinomio factorizado es:
x⁴ + 3·x³ - 3·x² - 11·x - 6 = (x + 1)²·(x - 2)·(x + 3)
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP11
- | Siguiente ›
Ejemplo, cómo calcular las raíces de un polinomio y factorizarlo