Problemas nº 9-c y 9-d de racionalización de denominadores - TP11
Enunciado del ejercicio nº 9 c y d
Racionalizar el denominador de las siguientes expresiones y simplificar si es posible:
| c) | 1 | = |
√a - ∛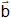 |
| d) | x + y - √x - y | = |
| x + y + √x - y |
Solución
c)
| 1 | = |
√a - ∛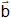 |
En el denominador podemos formar una diferencia de cuadrados con su conjugado:
√a + ∛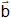
Multiplicamos numerador y denominador por el binomio propuesto:
Resolvemos:
| = | √a + ∛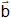 | = |
(√a)² - (∛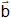 )² )² |
| = | √a + ∛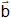 | = |
| a - ∛b² |
Resultado: no se puede racionalizar completamente el denominador.
d)
| x + y - √x - y | = |
| x + y + √x - y |
En el denominador podemos formar una diferencia de cuadrados con su conjugado:
(x + y) - √x - y
| = | x + y - √x - y | · | (x + y) - √x - y | = |
| x + y + √x - y | (x + y) - √x - y |
Resolvemos:
| = | (x + y - √x - y)² | = |
| (x + y)² - (√x - y)² |
| = | x² + x·y - x·√x - y + x·y + y² - y·√x - y - [x·√x - y + y·√x - y - (√x - y)²] | = |
| x² + 2·x·y + y² - (x - y) |
| = | x² + 2·x·y + y² - x·√x - y - y·√x - y - [x·√x - y + y·√x - y - (x - y)] | = |
| x² + 2·x·y + y² - x + y |
| = | x² + 2·x·y + y² - (x + y)·√x - y - [(x + y)·√x - y - x + y] | = |
| x² + 2·x·y + y² - x + y |
| = | x² + 2·x·y + y² - (x + y)·√x - y - (x + y)·√x - y + x - y | = |
| x² + 2·x·y + y² - x + y |
| = | x² + 2·x·y + y² + x - y - 2·(x + y)·√x - y |
| x² + 2·x·y + y² - x + y |
Expresamos el resultado:
| x + y - √x - y | = | x² + 2·x·y + y² + x - y - 2·(x + y)·√x - y |
| x + y + √x - y | x² + 2·x·y + y² - x + y |
Resolvió: Ricardo Santiago Netto. Argentina
Ejemplo, cómo racionalizar denominadores de polinomios
![]()