Problema nº 3 de sistemas de ecuaciones con dos incágnitas, aplicar determinantes - TP04

Enunciado del ejercicio nº 3

Determinar para qué valores del parámetro "k" el siguiente sistema tiene soluciones positivas:

Solución

Nos pide que:

x > 0 e y > 0

Aplicamos determinantes:

Primero calculamos el determinante del sistema:

Δ = 2·5 - 3·7

Δ = 10 - 21

Δ = -11

El determinanate del sistema es negativo, por lo tanto, los determinantes de "x" e "y" deben ser negativos para que las soluciones sean positivas.

Δₓ < 0 ∧ Δ_y < 0

Hallamos los determinantes:

Δₓ = 5·k - 13·7

Δₓ = 5·k - 91 < 0

5·k - 91 < 0

5·k < 91

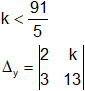
Δ_y = 2·13 - 3·k

Δ_y = 26 - 3·k < 0

26 - 3·k < 0

3·k > 26

Resultado, los valores del parámetro "k" son:

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP04
• | Siguiente ›

Ejemplo, cómo aplicar determinantes