Guía nº 4 de ejercicios resueltos de sistemas de ecuaciones con dos y tres incágnitas
Resolver los siguientes ejercicios
� Ver resolución de los ejercicios al pie de la página
Problema nº 1
Determinar si las siguientes ecuaciones con tres incógnitas son de primer grado:
a) (x - 2·y + z)² + 4·x·y = 2·x·z - 4·y·z
b) ![]()
• Respuesta:
a) La ecuación es de segundo grado en todas sus variables;
b) La ecuación es de segundo grado en todas sus variables;
Problema nº 2
Determinar para qué valores del parámetro "k" el siguiente sistema no tiene solución:
![]()
• Respuesta: k = 2
Problema nº 3
Determinar para qué valores del parámetro "k" el siguiente sistema tiene soluciones positivas:
![]()
• Respuesta:
![]()
Problema nº 4
Resolver los siguientes sistemas de ecuaciones con tres incógnitas:
a)
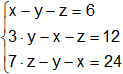
b)
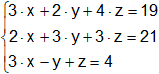
c)
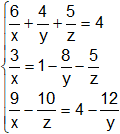
• Respuesta:
a) x = 39; y = 21; z = 12;
b) x = 3; y = 5; z = 0;
c) x = 3; y = 4; z = 5.
Problema nº 5
Dos personas aportan capitales a una empresa, la diferencia de aportes representa un tercio del capital conjunto y el doble de uno de los aportes menos el otro es de $ 60.000. ¿Cuál es el capital integrado?
• Respuesta: x + y = $ 60.000
Problema nº 6
¿Para qué valores reales "a" y "b" el siguiente sistema es determinado, indeterminado o incompatible?
![]()
• Respuesta: a·b ≠ 12; a·b = 12 ∧ a ≠ 16 ∧ b ≠ ¾; a·b = 12 ∧ a = 16 ∧ b = ¾
Problema nº 7
¿Para qué valores de n ∈ Z la solución del siguiente sistema satisface la condición x > 0 e y < 0?:
![]()
• Respuesta:
![]()
Problema nº 8
Si a ambos términos de la fracción 4/9 se les suma cierto número entero se obtiene 9/14. ¿Cuál es ese número entero?
• Respuesta: 5
Bibliografía:
"Matemática preuniversitaria". Leonor E. Carvajal. UTN - FRBA. Argentina.
Autor: Ricardo Santiago Netto. Argentina