Problema nº 5 de sistemas de ecuaciones con dos incágnitas - TP04
Enunciado del ejercicio nº 5
Dos personas aportan capitales a una empresa, la diferencia de aportes representa un tercio del capital conjunto y el doble de uno de los aportes menos el otro es de $ 60.000. ¿Cuál es el capital integrado?
Solución
El enunciado, puesto en ecuaciones, nos dice que:
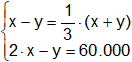
De la primera ecuación despejamos una de las incógnitas:
3·(x - y) = x + y
3·x - 3·y = x + y
3·x - x = 3·y + y
2·x = 4·y
x = 2·y
Reemplazamos en la segunda ecuación:
2·x - y = 60.000
2·(2·y) - y = 60.000
4·y - y = 60.000
3·y = 60.000
y = 60.000/3
y = 20.000
Con el valor de y reemplazamos en la segunda ecuación:
2·x - y = 60.000
2·x - 20.000 = 60.000
2·x = 60.000 + 20.000
2·x = 80.000
x = 80.000/2
x = 40.000
Resultado, el capital integrado es la suma de "x" e "y":
x + y = 40.000 + 20.000
x + y = $ 60.000
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP04
- | Siguiente ›
Ejemplo, cómo resolver ecuaciones