Problema nº 4 de sistemas angulares, convertir ángulos del sistema sexagesimal al sistema circular - TP01

Enunciado del ejercicio nº 4

Expresar en radianes los siguientes ángulos:

a) 90°

b) 45°

c) 30°

d) 75°

e) 120°

f) 150°

g) 2 giros

h) 300°

Solución

Los ángulos están dados en el sistema sexagesimal.

a)

α = 90°

Lo pasamos al sistema circular:

180° = π

α = π/2 rad = 1,570796327 rad

b)

α = 45°

Lo pasamos al sistema circular:

180° = π

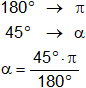
α = π/4 rad = 0,785398163 rad

c)

α = 30°

Lo pasamos al sistema circular:

180° = π

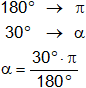
α = π/6 rad = 0,523598776 rad

d)

α = 75°

Lo pasamos al sistema circular:

180° = π

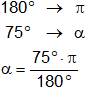
α = 1,308996939 rad

e)

α = 120°

Lo pasamos al sistema circular:

180° = π

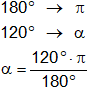
α = 2,094395102 rad

f)

α = 150°

Lo pasamos al sistema circular:

180° = π

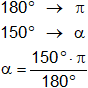
α = 2,617993878 rad

g)

α = 2 giros = 2·360° = 720°

Lo pasamos al sistema circular:

180° = π

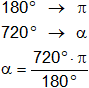
α = 4·π rad = 12,56637061 rad

h)

α = 300°

Lo pasamos al sistema circular:

180° = π

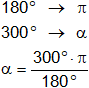
α = 5,235987756 rad

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP01
• | Siguiente ›

Ejemplo, cómo convertir ángulos del sistema sexagesimal al sistema circular