Problema nº 1 de trigonometría, lados de un triángulo - TP02

Enunciado del ejercicio nº 1

Calcular el otro lado del triángulo ABC, empleando el Teorema del coseno y tablas de valores naturales:

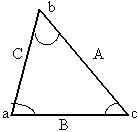
Desarrollo

Datos:

Fórmulas:

Teorema del coseno: "El cuadrado de un lado de un triángulo es igual a la suma de los cuadrados de los otros dos lados menos el doble del producto de dichos lados por el coseno del ángulo que forman".

C² = A² + B² - 2·A·B·cos c

A² = B² + C² - 2·B·C·cos a

B² = A² + C² - 2·A·C·cos b

Solución

a)

Aplicando el Teorema del Coseno:

C² = A² + B² - 2·A·B·cos c

C² = (11 cm)² + (6 cm)² - 2·(11 cm)·(6 cm)·cos 42°

C² = 121 cm² + 36 cm² - 132 cm²·0,7431

C² = 58,9049 cm²

Resultado (a):

C = 7,675 cm

b)

Aplicando el Teorema del Coseno:

B² = A² + C² - 2·A·C·cos b

B² = (7 m)² + (8 m)² - 2·(7 m)·(8 m)·cos 52° 20'

B² = 49 m² + 64 m² - 112 m²·0,6111

B² = 44,5605 m²

Resultado (b):

B = 6,675 m

c)

Aplicando el Teorema del Coseno:

A² = B² + C² - 2·B·C·cos a

A² = (10 cm)² + (15 cm)² - 2·(10 cm)·(15 cm)·cos 123° 40'

A² = 100 cm² + 225 cm² - 300 cm²·(-0,5544)

A² = 491,3081 cm²

Resultado (c):

A = 22,165 cm

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP02
• | Siguiente ›

Ejemplo, cómo calcular los lados de un triángulo