Problema nº 2 de trigonometría, aplicar identidades trigonométricas - TP02

Enunciado del ejercicio nº 2

Resolver las siguientes identidades:

a)

b) (sen α + cos α)² + (cos α - sen α)² = 2

c)

d) sen⁴ α - sen² α = cos⁴ α - cos² α

e)

f)

g) cos (α + β)·cos (α - β) = cos² α - sen² β

h)

i)

Solución

a)

∎

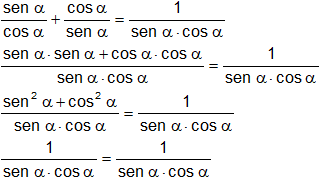
b)

sen² α + 2·(sen α)·(cos α) + cos² α + sen² α - 2·(sen α)·(cos α) + cos² α = 2

sen² α + cos² α + sen² α + cos² α = 2

(sen² α + cos² α) + (sen² α + cos² α) = 2

1 + 1 = 2 ∎

c)

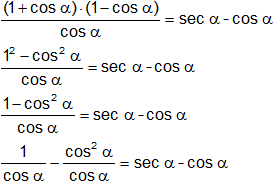
sec α - cos α = sec α - cos α ∎

d)

sen⁴ α - sen² α = cos⁴ α - cos² α

(sen² α)² - sen² α = cos⁴ α - cos² α

(1 - cos² α)² - (1 - cos² α) = cos⁴ α - cos² α

(1² - 2·1·cos² α + cos⁴ α) - (1 - cos² α) = cos⁴ α - cos² α

1 - 2·cos² α + cos⁴ α - 1 + cos² α = cos⁴ α - cos² α

-cos² α + cos⁴ α = cos⁴ α - cos² α ∎

e)

∎

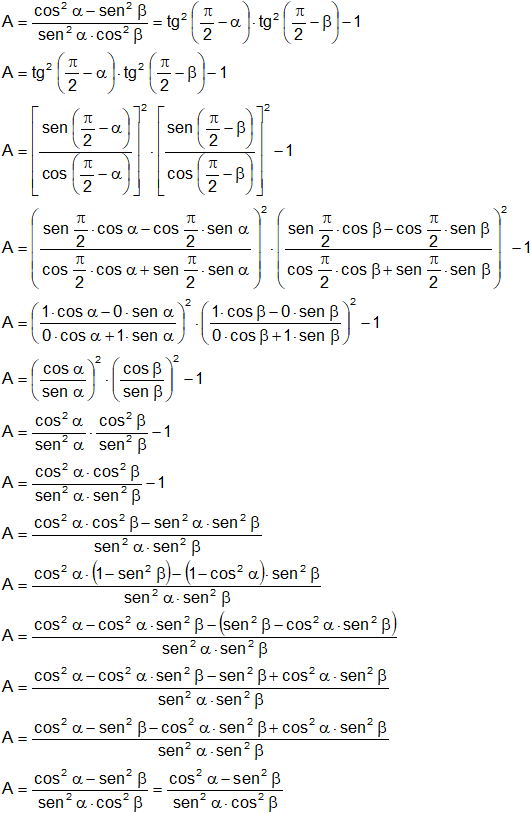
f)

Operamos con el primer término y al segundo lo dejamos fijo:

Simplificamos:

∎

g)

cos (α + β)·cos (α - β) = cos² α - sen² β

(cos α·cos β - sen α·sen β)·(cos α·cos β + sen α·sen β) = cos² α - sen² β

(cos α·cos β)² - (sen α·sen β)² = cos² α - sen² β

cos² α·cos² β - sen² α·sen² β = cos² α - sen² β

cos² α·(1 - sen² β) - (1 - cos² α)·sen² β = cos² α - sen² β

cos² α - cos² α·sen² β - (sen² β - cos² α·sen² β) = cos² α - sen² β

cos² α - cos² α·sen² β - (sen² β - cos² α·sen² β) = cos² α - sen² β

cos² α - sen² β = cos² α - sen² β ∎

h)

A =

Operamos con el primer término y al segundo lo dejamos fijo, reemplazamos:

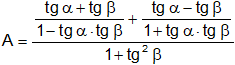
Sumamos las fracciones del numerador:

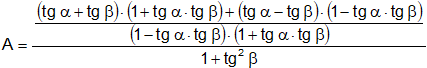
Aplicamos la propiedad distributiva del producto con respecto a la suma y a la resta:

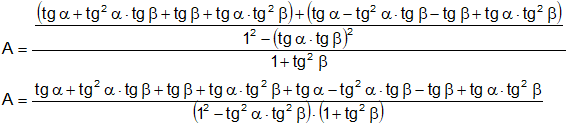
Agrupamos por monomios en el numerador:

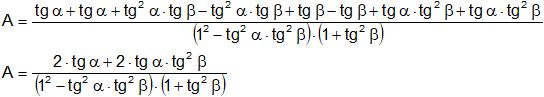
Extraemos factor común:

Simplificamos:

∎

i)

cos² α = cos² α ∎

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP02
• | Siguiente ›

Ejemplo, cómo aplicar identidades trigonométricas