Problema nº 4 de trigonometría, lados y ángulos de triángulos - TP02

Enunciado del ejercicio nº 4

Resolver los siguientes triángulos:

Desarrollo

Datos:

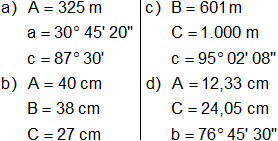
Fórmulas:

Teorema del Seno: "En todo triángulo sus lados son proporcionales a los senos de los ángulos opuestos".

Teorema del Coseno:

A² = B² + C² - 2·B·C·cos a

A + B + C = 180° (suma de los ángulos interiores de un triángulo)

Esquema:

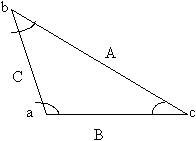
Solución

a)

La suma de los ángulos interiores de un triángulo es:

a + b + c = 180°

b = 180° - a - c

b = 180° - 30° 45' 20" - 87° 30'

b = 61° 44' 40"

Aplicando el Teorema del seno:

A/sen a = C/sen c

C = A·sen c/sen a

C = (325 m·sen 87° 30')/(sen 30° 45' 20")

C = (325 m·0,9990)/0,5114

C = 634,935 m

Aplicando el Teorema del seno:

A/sen a = B/sen b

B = A·sen b/sen a

B = (325 m·sen 61° 44' 40")/(sen 30° 45' 20")

B = (325 m·0,8808)/0,5114

B = 559,812 m

b)

Aplicando el Teorema del Coseno:

A² = B² + C² - 2·B·C·cos a

B² + C² - A² = 2·B·C·cos a

cos a = (B² + C² - A²)/2·B·C

cos a = [(38 cm)² + (27 cm)² - (40 cm)²]/2·(38 cm)·(27 cm)

cos a = (1.444 cm² + 729 cm² - 1.600 cm²)/(2.052 cm²)

cos a = (573 cm²)/(2.052 cm²)

cos a = 0,2792

a = arccos 0,2792

a = 73° 47' 7"

Aplicando el Teorema del Coseno:

B² = A² + C² - 2·A·C·cos b

A² + C² - B² = 2·A·C·cos b

cos b = (A² + C² - B²)/2·A·C

cos b = [(40 cm)² + (27 cm)² - (38 cm)²]/2·(40 cm)·(27 cm)

cos b = (1.600 cm² + 729 cm² - 1.444 cm²)/(2.160 cm²)

cos b = (885 cm²)/(2.160 cm²)

cos b = 0,4097

b = arccos 0,4097

b = 65° 48' 45"

La suma de los ángulos interiores de un triángulo es:

a + b + c = 180°

c = 180° - a - b

c = 180° - 73° 47' 7" - 65° 48' 45"

c = 40° 24' 8"

c)

Aplicando el Teorema del Seno:

C/sen c = B/sen b

sen b = (B/C)·sen c

sen b = (601 m/1.000 m)·sen 95° 02' 08"

sen b = 0,601·0,9961

sen b = 0,5987

b = arcsen 0,5987

b = 36° 46' 32"

La suma de los ángulos interiores de un triángulo es:

a + b + c = 180°

a = 180° - b - c

a = 180° - 36° 46' 32" - 95° 02' 08"

a = 48° 11' 20"

Aplicando el Teorema del Seno:

A/sen a = C/sen c

A = C·sen a/sen c

A = (1.000 m·sen 48° 11' 20")/(sen 95° 02' 08")

A = (1.000 m·0,7453)/0,9961

A = 748,23 m

d)

Aplicando el Teorema del Coseno:

B² = A² + C² - 2·A·C·cos b

B² = (12,33 cm)² + (24,05 cm)² - 2·(12,33 cm)·(24,05 cm)·cos 76° 45' 30"

B² = 152,0289 cm² + 578,4025 cm² - 593,073 cm²·0,2291

B² = 594,582801 cm²

B = 24,38 cm

Aplicando el Teorema del Seno:

C/sen c = B/sen b

sen c = (C/B)·sen b

sen c = (24,05 cm/24,38 cm)·sen 76° 45' 30")

sen c = 0,9863·0,9734

sen c = 0,9601

c = arctg 0,9601

c = 0,7650

c = 43° 49' 59"

La suma de los ángulos interiores de un triángulo es:

a + b + c = 180°

a = 180° - c - b

a = 180° - 43° 49' 59" - 76° 45' 30"

a = 59° 24' 31"

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP02
• | Siguiente ›

Ejemplo, cómo calcular los lados y los ángulos de triángulos mediante trigonometría