Problema nº 3 de trigonometría, lados y ángulos de triángulos - TP02

Enunciado del ejercicio nº 3

Resolver los siguientes triángulos rectángulos:

Desarrollo

Datos:

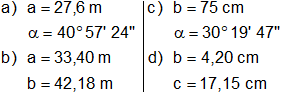
Fórmulas:

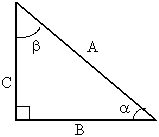
A + B + C = 180° (suma de los ángulos interiores de un triángulo)

sen θ = Cateto opuesto/Hipotenusa.

cos θ = Cateto adyacente/Hipotenusa.

tg θ = Cateto opuesto/Cateto adyacente

h² = a² + b²

Esquema:

Solución

a)

sen α = C/A

C = A·sen α

C = 27,6 m·sen (40° 57' 24")

C = 27,6 m·0,655

C = 18,089 m

tg α = B/C

B = C·tg α

B = 27,6 m·tg (40° 57' 24")

B = 27,6 m·0,868

B = 23,9568 m

α + β + 90° = 180°

β = 180° - α - 90°

β = 180° - 40° 57' 24" - 90°

β = 49° 2' 36"

b)

cos β = C/A

arccos (C/A) = β

β = arccos (42,18 m/33,40 m)

β = arccos 1,26287

β = 51° 37' 35"

α + β + 90° = 180°

α = 180° - β - 90°

α = 38° 22' 25"

Aplicando el teorema de Pitágoras:

A² = B² + C²

B² = C² - A²

B² = (42,18 m)² - (33,40 m)²

B² = 1.779,15 m² - 1.115,56 m²

B² = 663,59 m²

B = 25,76 m

c)

cos α = B/A

A = B/cos α

A = 75 cm/cos (30° 19' 47")

A = 75 cm/0,863

A = 86,89 cm

tg α = C/B

C = B·tg α

C = 75 cm·tg (30° 19' 47")

C = 75 cm·0,585

C = 43,88 cm

α + β + 90° = 180°

β = 180° - α - 90°

β = 180° - 30° 19' 47" - 90°

β = 59° 40' 13"

d)

tg α = C/B

arctg (C/B) = α

α = arctg (17,15 cm/4,20 cm)

α = arctg 4,083

α = 76° 14' 21"

tgβ = B/C

arctg (B/C) = β

β = arctg (4,20 cm/17,15 cm)

β = arctg 0,24489796

β = 13° 45' 39"

A² = B² + C²

A² = (17,15 cm)² + (4,20 cm)²

A² = 294,12 cm² + 17,64 cm²

A² = 311,76 cm²

A = 17,66 cm

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP02
• | Siguiente ›

Ejemplo, cómo calcular los lados y los ángulos de triángulos mediante trigonometría