Problema nº 2-a de trigonometría, funciones trigonométricas - TP03
Enunciado del ejercicio nº 2-a
Calcular el valor de "x":
| x = | sen 30° - sen 60° |
| sen 30° + sen 60° |
Solución
Recordamos la tabla:
| Grados | 0° | 30° | 45° | 60° | 90° |
| Radianes | 0 | π/6 | π/4 | π/3 | π/2 |
| Seno | 0 | ½ | ½·√2 | √3/2 | 1 |
| Coseno | 1 | √3/2 | ½·√2 | ½ | 0 |
| Tangente | 0 | 1/√3 | 1 | √3 | ∞ |
| x = | sen 30° - sen 60° |
| sen 30° + sen 60° |
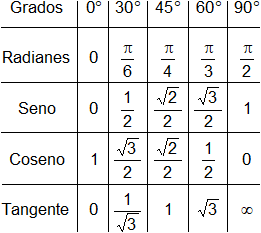
Reemplazamos por los valores de la tabla:
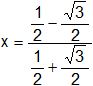
Sumamos las fracciones en el numerador y en el denominador:
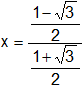
Expresamos la división principal como un producto:
Simplificamos:
Racionalizamos el denominador:
| x = | 1 - √3 | · | 1 - √3 |
| 1 + √3 | 1 - √3 |
| x = | 1² - 2·1·√3 + (√3)² |
| 1 - 3 |
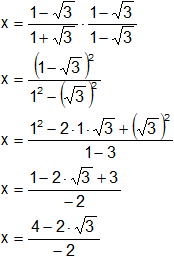
Extraemos factor común "-2" en el numerador:
Simplificamos:
Expresamos el resultado:
x = 
- 2
Resolvió: Ricardo Santiago Netto. Argentina
Ejemplo, cómo aplicar funciones trigonométricas