Problema nº 2 de trigonometría, funciones trigonométricas y sus inversas - TP05

Enunciado del ejercicio nº 2

En los siguientes casos calcular "x":

a) x = sen 38° 15'

b) cotg x = 0,57735

c) sen x = 0,0364

d) x = cos 72° 05' 15"

e) sen x = -(3^½/2)

f) tg x = 0,8699

g) x = tg 3° 19' 25"

h) cos x = -0,68236

i) sen x = 0,5466

j) x = cotg 29° 19'

k) sec x = 22

l) cos x = 0,1175

m) x = tg 90°

n) tg x = 3,25

o) sen x = 0,9807

p) x = cos 75°

q) cosec x = -3,5

r) cos x = 0,7729

s) x = cos π/12

t) tg x = 1,7302

u) x = sen 15°

v) cos x = 0,4893

w) x = tg 75°

x) cotg x = 0,6749

Solución

Estos ejercicios se resolvieron empleando una planilla de cálculo.

a)

x = sen 38° 15'

Expresamos el ángulo a grados con dos decimales:

α = 38° 15'

α = 38° + (15/60)°

α = 38,25°

x = sen 38,25°

Resolvemos:

x = 0,619093949

b)

cotg x = 0,57735

Para hallar "x" empleamos la función inversa:

x = arccotg 0,57735

Resolvemos:

x = 1,047197753 rad

c)

sen x = 0,0364

Para hallar "x" empleamos la función inversa:

x = arcsen 0,0364

Resolvemos:

x = 0,036408043 rad

d)

x = cos 72° 05' 15"

Expresamos el ángulo a grados con dos decimales:

α = 72° 5' 15"

α = 72° 5' + (15/60)'

α = 72° 5' + 0,25'

α = 72° 5,25'

α = 72° + (5,25/60)°

α = 72° + 0,0875°

α = 72,0875°

x = cos 72,0875°

Resolvemos:

x = 0,307564216

e)

sen x = -(3^½/2)

Para hallar "x" empleamos la función inversa:

x = arcsen -(3^½/2)

Resolvemos:

x = arcsen -0,866025404

x = -60°

f)

tg x = 0,8699

Para hallar "x" empleamos la función inversa:

x = arctg 0,8699

Resolvemos:

x = 0,854862134 rad

g)

x = tg 3° 19' 25"

Expresamos el ángulo a grados con dos decimales:

α = 3° 19' 25"

α = 3° 19' + (25/60)'

α = 3° 19' + 0,417'

α = 3° 19,417'

α = 3° + (19,417/60)°

α = 3° + 0,3236°

α = 3,3236°

x = tg 3,3236°

Resolvemos:

x = 0,05807

h)

cos x = -0,68236

Para hallar "x" empleamos la función inversa:

x = arccos -0,68236

Resolvemos:

x = 2,3218 rad

i)

sen x = 0,5466

Para hallar "x" empleamos la función inversa:

x = arcsen 0,5466

Resolvemos:

x = 0,5783 rad

j)

x = cotg 29° 19'

Expresamos el ángulo a grados con dos decimales:

α = 29° 19'

α = 29° + (19/60)°

α = 29° + 0,3167°

α = 29,3167°

x = cotg 29,3167°

Resolvemos:

x = 1,7808

k)

sec x = 22

Para calcular el "arcsec" se emplea la relación entre la "sec" y el "cos".

cos x = 0,045454545

Para hallar "x" empleamos la función inversa:

x = arccos 0,045454545

Resolvemos:

x = 1,5254 rad

l)

cos x = 0,1175

Para hallar "x" empleamos la función inversa:

x = arccos 0,1175

Resolvemos:

x = 1,453 rad

m)

x = tg 90°

x = ∞

n)

tg x = 3,25

Para hallar "x" empleamos la función inversa:

x = arctg 3,25

Resolvemos:

x = 1,2723 rad

o)

sen x = 0,9807

Para hallar "x" empleamos la función inversa:

x = arcsen 0,9807

Resolvemos:

x = 1,3740 rad

p)

x = cos 75°

Resolvemos:

x = 0,2588

q)

cosec x = -3,5

Para calcular el "arccosec" se emplea la relación entre la "cosec" y el "sen".

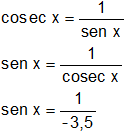
sen x = -0,285714286

Para hallar "x" empleamos la función inversa:

x = arcsen -0,285714286

Resolvemos:

x = -0,2898 rad

r)

cos x = 0,7729

Para hallar "x" empleamos la función inversa:

x = arccos 0,7729

Resolvemos:

x = 0,6874 rad

s)

x = cos π/12

Resolvemos:

x = 1,3059

t)

tg x = 1,7302

Para hallar "x" empleamos la función inversa:

x = arctg 1,7302

Resolvemos:

x = 1,0467 rad

u)

x = sen 15°

Resolvemos:

x = 0,2588

v)

cos x = 0,4893

Para hallar "x" empleamos la función inversa:

x = arccos 0,4893

Resolvemos:

x = 1,0595 rad

w)

x = tg 75°

Resolvemos:

x = 3,7321

x)

cotg x = 0,6749

Para hallar "x" empleamos la función inversa:

x = arccotg 0,6749

Resolvemos:

x = 0,9771 rad

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP05
• | Siguiente ›

Ejemplo, cómo aplicar funciones trigonométricas y sus inversas