Problema nº 6 de trigonometría, aplicar y hallar funciones trigonométricas - TP06
Enunciado del ejercicio nº 6
Calcular sen 2·a y cos 2·a siendo:
sen a = ⅔
Con: 0 < a < π/2
Solución
Recordamos la tabla:
| Grados | 0° | 30° | 45° | 60° | 90° |
| Radianes | 0 | π/6 | π/4 | π/3 | π/2 |
| Seno | 0 | ½ | √2/2 | √3/2 | 1 |
| Coseno | 1 | √3/2 | √2/2 | ½ | 0 |
| Tangente | 0 | 1/√3 | 1 | √3 | ∞ |
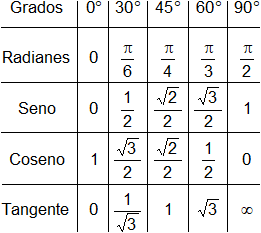
sen 2·a = 2·(sen a)·(cos a)
Según la condición todas las funciones son positivas.
cos a = √1 - sen² a = √1 - (⅔)² = √1 - 4/9 = √(9 - 4)/9 = √5/9 = ⅓·√5
Luego:
sen 2·a = 2·⅔·(√5/3)
sen 2·a = 4·√5/9
Finalmente:
cos 2·a = cos² a - sen² a
cos 2·a = (√5/3)² - ⅔²
cos 2·a = 5/9 - 4/9
cos 2·a = ⅑
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP06
- | Siguiente ›
Ejemplo, cómo aplicar y hallar funciones trigonométricas