Guía nº 1 de ejercicios resueltos de sistemas de ecuaciones lineales
Resolver los siguientes ejercicios
� Ver resolución de los ejercicios al pie de la página
Problema nº 1
Resolver los siguientes sistemas de ecuaciones lineales por los métodos de:
I) Igualación
II) Sustitución
III) Reducción
IV) Determinantes
V) Graficar
a)
![]()
b)
![]()
c)
![]()
d)
![]()
e)
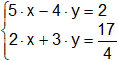
f)
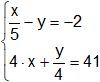
g)
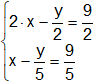
h)
![]()
i)
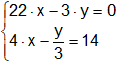
j)
![]()
• Respuesta:
a) P(-2; 5); m₁ = 3/2; b₁ = 8; m₂ = -5/4; b₂ = 5/2;
b) P(31/14; -22/7); m₁ = 4; b₁ = -12; m₂ = -2/3; b₂ = -5/3;
c) P(-3; 1); m₁ = -3; b₁ = -8; m₂ = 2/5; b₂ = 11/5;
d) P(3; 2); m₁ = 4/3; b₁ = -2; m₂ = -5; b₂ = 17;
e) P(1; ¾); m₁ = 5/4; b₁ = -1/2; m₂ = -2/3; b₂ = 17/12;
f) P(10; 4); m₁ = 1/5; b₁ = 2; m₂ = -16; b₂ = 164;
g) P(0; -9); m₁ = 4; b₁ = -9; m₂ = 5; b₂ = -9;
h) P(11; 0); m₁ = 1/2; b₁ = -11/2; m₂ = -1/2; b₂ = 11/2;
i) P(9; 66); m₁ = 22/3; b₁ = 0; m₂ = 12; b₂ = -42;
j) el sistema no tiene solución; m₁ = -1/2; b₁ = 0; m₂ = -1/2; b₂ = 7/5
Autor: Ricardo Santiago Netto. Argentina
Problemas resueltos:
Gráfica, punto de intersección, ordenada al origen y pendiente